How do we know the Riemann Sum gives us the area under the curve?

Question

I'm currently learning calculus (high school senior), and I am not comfortable with the idea that the limit of the sums of rectangles actually converges to the area under the curve. I know it looks like it does, but how do we know for sure? Couldn't the tiny errors beneath/over the curve accumulate as we add more and more rectangles? What's troubling me is the whole Pi = 4 thing with the staircase approximating a circle pointwise, and how it's wrong and the perimeter of the staircase shape does not approach the circumference of the circle, even though pointwise it does approach a circle. So how are the increasingly many, increasingly small errors in Riemann sums any different? How do we know the error in each step decreases faster than the number of errors increases? I would really like to see a proof of this.

Thanks so much!

Answer 1

This actually is a very good question and something that really takes a two-prong answer to fully do it justice.

---

PART 1.

You are right to be skeptical and, I'd say, this is yet another of those times where that the "standard" maths curriculum and expositions do a really great job of making something easy, hard. You should trust your gut here, not your teacher.

The answer is simple: no, you cannot "prove" this, unless you have an independent formal definition of "area" that is separate from the Riemann integral and comprehensive enough to handle these situations on its own. Such a definition can be made: it's called Lebesgue Measure, but it takes a bit more mathematical machinery than is available at this point in exposition to make it cook.

Basically, Lebesgue measure is a function that takes a single input argument which is an entire set of points on the plane, i.e. $S$, interpreted as a solid area and not merely the boundary, and tells you its area, $\mu(S)$. This $S$ would be, in your case, the solid plane figure that is colored in on the graphs in your calculus textbook as being the "area under the curve". There is no integrals involved in its definition though, as I'd say, we'd need to expose a considerable amount of new machinery to build this. But if you do that, then take my word that you can prove that

$$\mu(S) = \int_{a}^{b} f(x)\ dx$$

where the right hand is a Riemann integral and the $S$ is as I described for this particular situation, when said Riemann integral exists.

ADD: As @Paramanand Singh mentions in the comments, there are simpler ways to define the area that may be more digestible at this point, though they do not cover as many cases as the Lebesgue measure. The Borel measure and Jordan pseudo-measure are two such options and I could attempt to describe them here if you wish or, you could ask another question in the vein of "What is a simple, integral-free definition of the area of a complicated plane figure that is digestible at or near the level of introductory calculus?" and I could then answer it with one or both of these.

---

PART 2.

This, of course, leads one to what a better way to introduce the integral should be, given we cannot at this stage do the necessary proof. And moreover, even if we could, then it would lead one to scratch one's head as to just why exactly we care to be creating this idea of "Riemann integral" in the first place when we already have a perfectly-good working construct for area.

And so, what I'd say is that a superior approach is to say that the Riemann integral is an explicit method to reconstruct a function from its derivative and, to make this clearer, we also need a better intuitive understanding of what a "derivative" means beyond the "tangent line" business that, while actually not bad at all, is itself also ruined by a poor explanation, too and which I could add still more details to get into, but I want to try and keep focus on the problem at hand. As Deane Yang mentioned in what was one of the posts that had a great influence in shaping my present attitude towards maths and especially maths education, here:

a better intuitive model for the "derivative" is that it is a kind of "sensitivity measurement": if I say that the derivative of a real-valued function of a real variable, $f$, has the value at the point $x$ of $f'(x)$, what that means intuitively is that if I "wiggle" $x$ back and forth a little bit, i.e. $\Delta x$, back and forth about this value, and I watch then the output value of $f$, i.e. $f(x)$, as though $f(x)$ were some instrument with a readout and $x$ a dial we could turn back and forth, then this $f(x)$ will likewise "wiggle" some other amount, i.e. $\Delta y$, and that

$$\Delta y \approx f'(x)\ \Delta x$$

provided $\Delta x$ is small - the accuracy of the approximation becoming as good as we like it if we make $\Delta x$ suitably smaller than whatever value we've been using so far: hence why we need to pass to a limit, a concept that, once more, can use some further elucidation. Or, to turn it around, $f'(x)$ is the "best" number to represent how much the output changes proportionally to the input, so long as we keep the input change small enough.

The Riemann integral, then, is the answer to this question:

• Give me a procedure that, if we are first given the derivative, $f$, to find a function $F$ that has it as its derivative, with the initial information that $F(a) = 0$, for some selected point $a$.

That is, it is in effect a constructive way to solve what in differential equations terminology would be called the initial-value problem, or IVP,

$$\frac{dF}{dx} = f, F(a) = 0$$

that proceeds as follows.

We are given the only starting information that $F(a) = 0$, and that $F' = f$. So suppose we are to construct the value of $F$ at a new point $b$ for which $b > a$. How may we try this, given what we've already discussed?

So now, think about what I just said about the meaning of the derivative, and ask yourself this question:

I know that $F'$ here is how sensitive it is to a small change. So suppose I were to now do a Zeno-like manoeuvre and hop a small amount $\Delta x$ from $a$ rightward along the real number line to $a + \Delta x$. What then should we guess for $F(a + \Delta x)$?

Well, if you got what I just mentioned, then you should come to that, since $F'(a)$ is proportionately how much $F$ will respond to a small change in its input around $a$, and what we are doing is exactly that: to make such a small change from $a$ to $a + \Delta x$, then we should likewise shift $F(a)$ to $F(a) + (F'(a) \Delta x)$, so that

$$\begin{align} F(a + \Delta x) &\approx F(a) + [F'(a)\ \Delta x]\\ &= F(a) + [f(a)\ \Delta x]\end{align}$$

. And then, we can do the same thing, and make another small "wiggle" from $a + \Delta x$ to $[a + \Delta x] + \Delta x$ (i.e. $a + 2\Delta x$), and we get

$$\begin{align}F([a + \Delta x] + \Delta x) &\approx F(a + \Delta x) + [F'(a + \Delta x)\ \Delta x]\\ &= F(a) + [f(a) + \Delta x] + [f(a + \Delta x)\ \Delta x]\end{align}$$

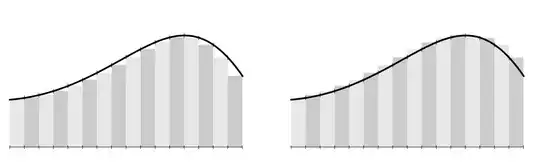
and if you continue on this way all the way until we get to $b$, or at least as close as possible, you see we have

$$F(b) \approx \sum_{n=0}^{N-1} f(a + n\Delta x)\ \Delta x$$

or, letting $x_i := a + i\Delta x$,

$$F(b) \approx \sum_{i=0}^{N-1} f(x_i)\ \Delta x$$

. Moreover, we can generalize this a bit further still to allow for irregular steps, which increases the flexibility a bit for, say, mildly discontinuous input functions $f$, and so we get

$$F(b) \approx \sum_{i=0}^{N-1} f(x_i)\ \Delta x_i$$

and we're almost there, all it takes now is a limit to get to...

$$F(b) = \lim_{||\Delta|| \rightarrow 0} \sum_i f(x_i)\ \Delta x_i$$

and if we introduce a bit of notation for this new concept now...

$$\int_{a}^{b} f(x)\ dx := \lim_{||\Delta|| \rightarrow 0} \sum_i f(x_i)\ \Delta x_i$$

which is...?

And by the way, is the Fundamental Theorem of Calculus much of a "surprise" now, or almost tautological, something that was by design, not a mystery to be solved? (This is pattern I also find crops up elsewhere where the best motivating reason for something is put after and not before - e.g. Cayley's theorem in abstract algebra.)

That is, the real surprise is not that we can use the Riemann sum to find an antiderivative - that's its whole point - but that this sum also can describe an area and that is, indeed, much less trivial to prove.

Answer 2

The Riemann integral (really Darboux' definition, as that is what is usually taught as "Riemann integral") is a purely analytical construction. It does not have any relation to "areas". What is important is that it satisfies some of the properties the "area under the curve" has (where it makes sense).

Sure, you can interpret the integal as the area below a curve, but Riemann's integral was defined precisely to handle (some) cases where that makes little sense, in a rigorous manner (Newton's, Leibnitz' "definitions" were quite handwavy). Note also that later definitions of integral (Lebesgue's, Stieltjes') have little or no visual connection to "areas", are even defined for cases where area makes no sense whatsoever.

Answer 3

In most, if not all, Calculus textbooks, the area under the curve is actually DEFINED to be the appropriate definite integral.

Answer 4

I think that Bernard made a good point in the comments under your question. So let me compile that into a short answer.

The trick is in working not with one, but with two slightly different Riemann sums - the lower and the upper Riemann sum. Consider the following figure:

I think we can agree that the lower Riemann sum $\check\Sigma$ (in the left figure) underestimates the actual area under the curve, and that the upper Riemann sum $\hat \Sigma$ (in the right figure) overestimates the actual area under the curve.

So we can agree that the actual area $A$ under the curve is somwhere between these sums:

$$\check\Sigma\le A\le \hat\Sigma.$$

Now, if we make the Riemann sum finer and finer (adding more rectangles, and making them thinner), the hope is that the lower and upper value come closer and closer to each other, and converge to a common value. If that would be the case, we could agree that this common value must be $A$, as $A$ was at all times trapped between these both sums.

So how do we know that the lower and the upper Riemann sum converge to the same value? The answer is: we don't! They do, in general, not converge to the same value! But they do for some functions, and these functions are then called Riemann integrable. These are the functions for which the Riemann sum is a valid tool to compute the area under the curve.

So the problem was now shifted to the question: "which functions are Riemann integrable?". And this is indeed a non-trivial question. Luckily, most functions that appear in everyday applications are in fact Riemann integrable. For example, continuous functions (on bounded intervals) or monotone functions are Riemann integrable, and one can prove this rigorously. This is usually done in an introductory analysis course for mathematicians. If you are interested in a proof: Wikipedia contains a proof of the fact that a functions is Riemann integrable (on a compact interval) if and only if it is continuous almost everywhere.