One day I saw human pyramid, then a question came to my mind which is "if there are $k$ rows in a human pyramid can we derive a formula to find the weight bore by any person??"
I started like this : Assume that weight of all persons is same, for simplicity let's say $1$. The weight of a person is borne by two lower persons equally. Let me introduce my notation $W(m,n)$ represents the weight bore by person in $m$th row , $n$th person from left.
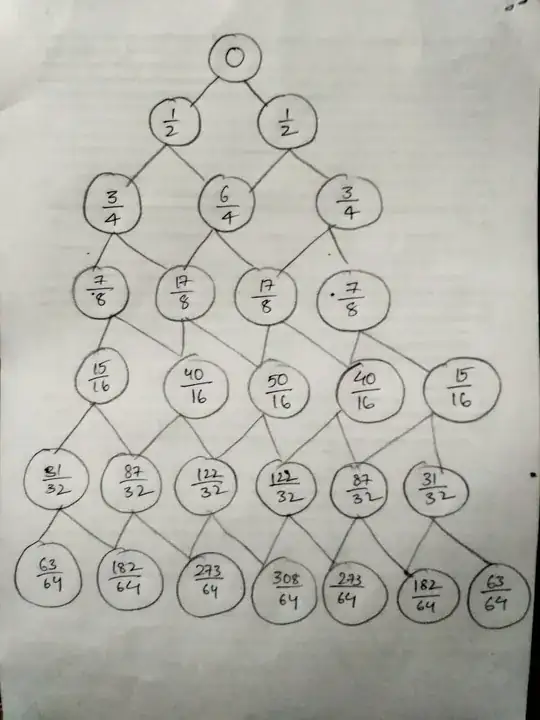
I put a image for some rows . I am thinking it is similar to Pascal's triangle and may be factorial may be involved in it!! but I got no leads in that direction.The number in the circle indicates the weight bore by that person. After working for some time I figured some properties they are:
$•$ If $m \not= n$ or $n \not=1$ then
$W(m,n)=\frac{W(m-1,n-1)+W(m-1,n)}{2} +1$
$•$ if $n=m$ or $n=1$ then
$W(m,m)=W(m,1)=\frac{2^{m-1}-1}{2^{m-1}}$
This tells us a interesting fact that no matter how many rows you have above you if are at bottoms row extreme point you will never have to bear more than your weight!!.
$•$ $W(m,1)+W(m,2)+....W(m,m)=W(m-1,1)+W(m-1,2)....W(m-1,m-1)+ m-1$
I figured only recursive formulas.I am trying to get a standard formula which would give weight borne by any person with out depending on recursion .Any help??