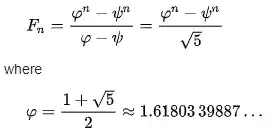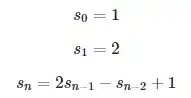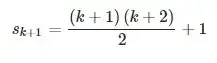how does one come up with these formulae?
There is no generic rule that could cover all imaginable recurrences, however there are specific types of recurrences for which one can work out solutions.
One such case where a formula can be given is the linear case (like with Fibonacci numbers), that can be approached by linear algebra: Suppose the recurrence has the form
$$
x_n = a_1 x_{n-1} + a_2 x_{n-2} +\cdots +a_k x_{n-k} = \sum_{j=1}^k a_j x_{n-j}
$$
for $n>k\geqslant 1$ where $x_1$, ..., $x_k$ are given numbers in some field $K$ and the $a_i$ are constants not depending on $n$.
To get an explicit representation for $x_n$, write the recurrence as:
$$
\underbrace{\left(\begin{array}{l}
x_{n\;\;\;}\\
x_{n-1}\\
\;\;\vdots\\
x_{n-k+2}\\
x_{n-k+1}\\
\end{array}\right)}_{\displaystyle{=:y_n}}
=\underbrace{\begin{pmatrix}
a_1 & a_2 & \cdots & a_{k-1} & a_k \\
1 & 0 & \cdots & 0 & 0 \\
0 & 1 & \cdots & 0 & 0 \\
\vdots &&\ddots&&\vdots \\
0 & 0 & \cdots & 1 & 0 \\
\end{pmatrix}}_{\displaystyle{=:A\in K^{k\times k}}}
\cdot
\underbrace{\left(\begin{array}{l}
x_{n-1}\\
x_{n-2}\\
\;\;\vdots\\
x_{n-k+1}\\
x_{n-k}\\
\end{array}\right)}_{\displaystyle{=:y_{n-1}}}
$$
so that it takes the form
$$
y_n = Ay_{n-1} = A^{n-k}y_k
$$
Hence we'll are left with determining $n$-th powers of a square matrix $A$. Now suppose $A$ has $k$ different eigenvectors $v_j$ and we know all of them, including the corresponding eigenvalues $\lambda_j$.
Then we can write:
$$
y_k = \sum_{j=1}^k \beta_j v_j
= V\begin{pmatrix}
\beta_k\\
\vdots\\
\beta_1\end{pmatrix}
= \begin{pmatrix}v_k&\cdots&v_1\end{pmatrix}\cdot\begin{pmatrix}
\beta_k\\
\vdots\\
\beta_1\end{pmatrix}
$$
where the $\beta_j$ are scalars in the algebraic closure of $K$ and $V$ is a matrix with the eigenvectors of $A$ as columns.
Hence:
$$
y_n = A^{n-k}y_k
= A^{n-k}\Big(\sum_{j=1}^k \beta_j v_j\Big)
= \sum_{j=1}^k \beta_j A^{n-k}v_j
= \sum_{j=1}^k \beta_j \lambda_j^{n-k}v_j \qquad (1)
$$
which leaves is with the computation of the $\beta_j$, the $v_j$ and the $\lambda_j$.
Once we determined the eigenvectors, we get the $\beta_j$ by means of:
$$
\begin{pmatrix}
\beta_k\\
\vdots\\
\beta_1\end{pmatrix}
= V^{-1}y_k
$$
Expanding the determinant of $A-\lambda E$ by expanding after it's top row, we find that all eigenvalues satisfy the characteristic equation
$$\lambda^k = \sum_{j=1}^k a_j\lambda^{k-j} = a_1\lambda^{k-1}+a_2\lambda^{k-2}+\cdots+a_{k-1}\lambda+a_k$$
From this we easily see that the eigenvectors of $A$ are:
$$v_j
= \left(\begin{array}{l}
\lambda_j^{k-1} \\
\;\;\vdots\\
\lambda_j^2 \\
\lambda_j \\
1 \\
\end{array}\right)
$$
Due to (1), in order to get $x_n$ we take the top component of $y_n$ to get:
$$
x_n = \sum_{j=1}^k \beta_j \lambda_j^{n-k}\lambda_j^{k-1}
= \sum_{j=1}^k \beta_j \lambda_j^{n-1} \qquad (2)
$$
Thus we are finished: Depending on the $a_j$, the eigenvalues can be computed explicitly or by numerical methods.
From the eigenvalues we get the Vandermonde-like matrix $V$ which we use to compute the coefficients $\beta_j$ from the
starting values $x_1$ ... $x_k$ so that we have determined all unknowns in (2).
2nd Order
This is the case $x_n = a_1x_{n-1}+a_2x_{n-2}$.
The matrix $V$ composed of the eigenvectors is:
$V=\begin{pmatrix}
\lambda_2 & \lambda_1\\
1&1\\
\end{pmatrix}$ with inverse
$$
V^{-1}
=\dfrac{1}{\lambda_2-\lambda_1}\begin{pmatrix}
1 & -\lambda_1\\
-1&\lambda_2\\
\end{pmatrix}
$$ so that
$$
\binom{\beta_2}{\beta_1}=\dfrac{1}{\lambda_2-\lambda_1}\binom{x_2-\lambda_1 x_1}{\lambda_2 x_1-x_2}
$$
and we arrive at
$$
x_{n+1}=\dfrac{(\lambda_2 x_1-x_2)\lambda_1^n + (x_2-\lambda_1 x_1)\lambda_2^n}{\lambda_2-\lambda_1}
$$
In the case of Fibonacci numbers, we have $a_1 = a_2 = x_1 = x_2 = 1$.
The characteristic equation is $\lambda^2 = \lambda + 1$ which has the Golden Ratio $\lambda_1=\varphi$ as solution as well as $\lambda_2=\psi=1-\varphi=-1/\varphi$. Plugging in:
$$\begin{align}
x_{n+1}
&=\dfrac{(\psi-1)\varphi^n + (1-\varphi)\psi^n}{\psi-\varphi} \\
&=\dfrac{-\varphi^{n+1} + \psi^{n+1}}{\psi-\varphi} \\
&=\dfrac{\varphi^{n+1} - \psi^{n+1}}{\varphi-\psi} \\
\end{align}$$
Coinciding Eigenvalues
An interesting / annoying case is when two or more eigenvalues are the same so that $V$ is not invertible, so that there is no straight forward way to determine the $\beta_i$. In that case we can still arrive at a solution if $K$ supports concepts like continuity. Take for example the 2-dimensional case from above over $\mathbb R$ or $\mathbb C$ with $\lambda=\lambda_1=\lambda_2$. We then write $\lambda_2=\lambda+\varepsilon$ and take $\lim_{\varepsilon\to0}$:
$$\begin{align}
x_{n+1}
&=\lim_{\varepsilon\to0}
\dfrac{(\lambda_2 x_1-x_2)\lambda_1^n + (x_2-\lambda_1 x_1)\lambda_2^n}{\lambda_2-\lambda_1}\\
&=\lim_{\varepsilon\to0}
\dfrac{x_1 \lambda (\lambda+\varepsilon) (\lambda^{n-1}-(\lambda+\varepsilon)^{n-1}) + x_2 ((\lambda+\varepsilon)^n - \lambda^n)}{\varepsilon}\\
&= -(n-1)\lambda^n x_1 + n\lambda^{n-1} x_2\\
\end{align}$$
Example: Take $x_{n+2} = 2x_{n+1} - x_n$ with characteristic polynomial $\lambda^2=2\lambda-1$. This has a double root at $\lambda=1$. The explicit formula is hence $x_{n+1}=n x_2 - (n-1)x_1$.