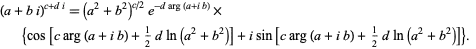I have taken a short course in analytic number theory and the following question had emerged: is the property $x^yx^z=x^{y+z}$ valid for any complex numbers $x, y$ and $z$? In fact, during the proof of prime number theorem given by D. J. Newman, this property is used but with real $x$ values. I tried to find some counterexamples using a complex number $x$, but I couldn't and by direct verification, I believe that it is true for any $x$ complex. Someone could assume Wolfram's definition: mathworld.wolfram.com/ComplexExponentiation.html I would appreciate any help.
-
1What does $x^y$ mean for arbitrary complex numbers $x$ and $y$? – José Carlos Santos Feb 27 '20 at 15:38
-
Someone could assume the same definition of Wolfram: http://mathworld.wolfram.com/ComplexExponentiation.html – Michel Faleiros Feb 27 '20 at 15:44
-
2That definition is proof that it holds. It was specifically so it would hold that we defined $e^{\theta i}$ as $\cos \theta + i \sin \theta$. Tedious trig and natural log properties can indeed show that the property holds – fleablood Feb 27 '20 at 15:52
-
1Also relevant, in the event that you defined exponentiation via the function $\text{exp}(z)$, one could expand the series for each as done here. – JMoravitz Feb 27 '20 at 15:54
-
I'm not sure that is so much direct, because of complex argument summation while the tedious trig to verify it. It sounds good, really the truth, but are you (@fleabood) sure that sum of arguments doesn't cause any trouble? By Euler series you (@JMoravitz) proof that for a real $x$ not a complex one. – Michel Faleiros Feb 27 '20 at 16:04
-
No problems. the trig identities are $\cos \theta \cos\beta - \sin \theta\sin\beta = \cos (theta + beta)$ and $\cos\theta \sin \beta + \cos\beta\sin\theta = \sin (\theta + beta)$ make everything work. and... oh, I see an error I made in my answer. Give me fifteen minutes. – fleablood Feb 27 '20 at 16:15
3 Answers
It's true.
In fact it was to preserve this basic property that was the basis of the definition of complex exponentiation.
Key points $\cos(\alpha + \beta) = \cos\alpha\cos\beta - \sin\alpha\sin\beta$ and $\sin(\alpha + \beta) = \cos\alpha\sin \beta + \sin\alpha\cos\beta$.
And of course that for real values $e^x e^y = e^{x+y}$ and $\ln M\ln N = \ln(M+N)$.
Taking the definition from Wolfram
So we need to prove that
$(a+bi)^{c+d i}(a+bi)^{g+hi} =$
$(a^2 + b^2)^{\frac c2}e^{-d\arg(a+bi)}\cdot\{\cos[c\arg(a+ib) + \frac 12 d\ln(a^2+b^2)] + i\sin[c\arg(a+ib) + \frac 12d(a^2 + b^2)]\}\times (a^2 + b^2)^{\frac g2}e^{-h\arg(a+bi)}\cdot\{\cos[g\arg(a+ib) + \frac 12 h\ln(a^2+b^2)] + i\sin[g\arg(a+ib) + \frac 12h(a^2 + b^2)]\}=$
$(a^2 + b^2)^{\frac c2}(a^2 + b^2)^{\frac g2}e^{-d\arg(a+bi)}e^{-h\arg(a+bi)}\cdot\{\cos[c\arg(a+ib) + \frac 12 d\ln(a^2+b^2)] + i\sin[c\arg(a+ib) + \frac 12d(a^2 + b^2)]\}\{\cos[g\arg(a+ib) + \frac 12 h\ln(a^2+b^2)] + i\sin[g\arg(a+ib) + \frac 12h(a^2 + b^2)]\}=$
$(a^2+b^2)^{\frac{c+g}2}e^{(-d-h)\arg(a+bi)}\cdot\{\cos[c\arg(a+ib) + \frac 12 d\ln(a^2+b^2)]\cos[g\arg(a+ib) + \frac 12 h\ln(a^2+b^2)]-\sin[c\arg(a+ib) + \frac 12d(a^2 + b^2)]\sin[g\arg(a+ib) + \frac 12h(a^2 + b^2)]\} + \{\sin[c\arg(a+ib) + \frac 12d(a^2 + b^2)]\cos[g\arg(a+ib) + \frac 12 h\ln(a^2+b^2)]+ \sin[g\arg(a+ib) + \frac 12h(a^2 + b^2)]\cos[c\arg(a+ib) + \frac 12 d\ln(a^2+b^2)]\}i=$
$(a^2+b^2)^{\frac{c+g}2}e^{-(d+h)\arg(a+bi)}\cdot(\cos\{[c\arg(a+ib) + \frac 12 d\ln(a^2+b^2)]+[g\arg(a+ib) + \frac 12 h\ln(a^2+b^2)]\} + \sin\{[c\arg(a+ib) + \frac 12 d\ln(a^2+b^2)]+[g\arg(a+ib) + \frac 12 h\ln(a^2+b^2)]\}i)=$
$(a^2+b^2)^{\frac{c+g}2}e^{-(d+h)\arg(a+bi)}\cdot(\cos\{[(c+g)\arg(a+ib) + \frac 12 (d+h)\ln(a^2+b^2)\} + \sin\{[(c+g)\arg(a+ib) + \frac 12 (d+h)\ln(a^2+b^2)\}i)=$
$(a+bi)^{(c+g) + (d+h)i}=$
$(a+bi)^{(c+di) + (g+hi)}$.
- 124,253
-
I agree with this proof, it sounds right. It only needs to fit the factors multiplying the trigonometric parts. In fact, jointing this proof with the proof mentioned by @JMoravitz required when multiplying theses factors the work is completed. Thank you! Me feeling now is that it is really true. – Michel Faleiros Feb 27 '20 at 16:25
-
Sorry, it is not necessary to use that proof mentioned by @JMoravitz, because you are multiplying real factors. – Michel Faleiros Feb 27 '20 at 16:29
It depends on the interpretation of $z^v$ for $z,v \in \mathbb C$. In case $z = 0$ we may define $0^v = 0$ for all $v$ although the formula $0^0 = 0$ may be questionable.
For $z \ne 0$ we can write $z = e^{\ln z}$, where $\ln z$ is any solution of $e^\omega = z$. It is well-known that there are infinitely many solutions which differ by integral multiples of $2\pi i$. However, based on the choice of a solution we can define $$z^v = e^{v \ln z} .$$ This is the definition in Wolfram although it is not made precise how the choice of $\ln z$ has to be done. However, note that if we replace the chosen $\ln z$ by $\ln z + 2n\pi i$, then we see with $v = a+ib$ $$e^{v (\ln z + 2n\pi i)} = e^{v \ln z}e^{2n\pi i v} = e^{v \ln z}e^{2n\pi a i}e^{-2n\pi b}$$ This is different from $e^{v \ln z}$ unless $b = 0$ and $a= k/n$ for some $k \in \mathbb Z$. Thus I believe it is not a good definition of $z^v$.
With a fixed choice of $\ln z$ we clearly get $$z^v z^w = e^{v \ln z} e^{w \ln z} = e^{v \ln z + w \ln z} = e^{(v+w)\ln z} = z^{v+w} .$$
Edited:
For $z \ne 0$ Wolfram uses $\arg (z)$ which denotes any solution of $ e^{i\omega} = z/\lvert z \rvert$. Any two solutions differ by an integral multiples of $2\pi$. Then $\ln z = \ln \lvert z \rvert + i \arg (z)$, where $\ln x$ for $x \in \mathbb R$ is the usual real logarithm. Thus $$z^v = e^{v (\ln \lvert z \rvert + i \arg (z)} = e^{v\ln \lvert z \rvert + i v \arg (z)} = e^{v\ln \lvert z \rvert} e^{i v \arg (z)} = \lvert z \rvert^v e^{i v \arg (z)} .$$ This is the formula in Wolfram. Note that the part $\lvert z \rvert^v = \lvert z \rvert^a e^{ib \ln \lvert z \rvert}$ does not depend on any choice of $\arg (z)$.
- 76,394
- 12
- 43
- 125
-
Nice comment @Paul Frost. So, the Wolfram's definition is good considering a fixed choice for the interval of $arg$ function. For any choice, it is important covers a length of $2\pi$ such that we are able to compute $z^v$ for arbitrary $v$ and $z$. (only a little correction above, $e^\omega=x$ should be $e^\omega=z$, shouldn't?) – Michel Faleiros Feb 27 '20 at 17:32
-
$\arg (z)$ can be chosen arbitrarily. Any two choices differ by an intgral multiple of $2\pi$. "Usually" one takes the principal value $\arg (z) \in [0,2\pi)$. You can replace $[0,2\pi)$ by any half-open interval $J$ of length $2\pi$. This gives continuity of $\arg (z)$ on a sliced plane, the slice going through $e^{ir}$, where $r \in J$ is the unique bounbdary point. However, there is no continuous $\arg$-function on the whole plane. I edited my answer to correct the mistake $e^\omega = x$. – Paul Frost Feb 27 '20 at 19:54
$$y\log x+z\log x=(y+z)\log x$$ seems valid in the complex too. This does not really depend on the definition of the logarithm and the antilogarithm.