0

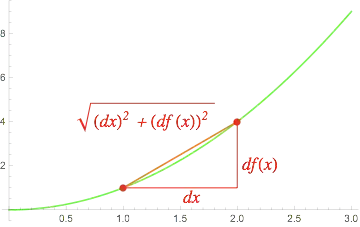
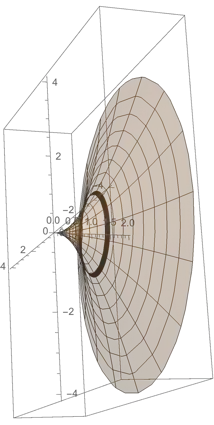
I am trying to prove the following statement:

Let $f:[a,b] \rightarrow R$ be an integrable function. Prove that the area of surface revolution obeys:

$$A = 2 \pi \int\limits^b_a f(x) \sqrt{1 + \bigg(\frac{df(x)}{dx}\bigg)^2}dx$$

I tried using the area of a cylinder but I couldn't get to a point where I got the integral.

David G. Stork
  • 29,774
Rolando González
  • 611
  • Each differential area is a ring of circumference $2 \pi f(x)$ and transverse length $\sqrt{1 + \left( \frac{df(x)}{dx}\right)^2}$. – David G. Stork Feb 26 '20 at 22:02
  • The only thing is how to get the transverse length, I can't join both ideas – Rolando González Feb 26 '20 at 22:14
  • draw the points $(x,y=f(x)),(x+dx, y=f(x+dx)= f(x)+f'(x)dx=y+dy)$, the horizontal segment $dx$ the vertical $dy$ the hypotenuse which is almost the arc made by the function .. – G Cab Feb 26 '20 at 22:21
  • It comes from the arc length formula, $\mathrm ds = \sqrt{1+\left(\dfrac{\mathrm dy}{\mathrm dx}\right)^2} , \mathrm dx$, which can be shown with the Pythagorean and Mean Value theorems. – KM101 Feb 26 '20 at 22:34
  • 1
    It is was introduced to me as the frustum of a cone. The area is the "slant height" times the circumference. $\sqrt {1+ f'(x)}\ dx$ is the slant height. $2\pi f(x)$ is the circumference. – user317176 Feb 26 '20 at 23:06
  • You may have a look at this answer : https://math.stackexchange.com/a/1692595/72031 – Paramanand Singh Feb 27 '20 at 08:04

1 Answers1

2

Each differential area is a ring of circumference $2 \pi f(x)$ and transverse length $\sqrt{(dx)^2 + (df(x))^2} = dx \sqrt{1 + \left(\frac{df(x)}{dx} \right)^2}$

enter image description here

enter image description here

David G. Stork
  • 29,774