Solution of $ax=a^x$

Question

When I studied math at my school (I was 16) I was studying system of linear equations, and equations of first or second order and I liked it very much (and I was good to xD) but one day I asked to myself how to solve equation of this kind $ax=a^x$ and ...I had no idea, I have felt completely disorientated.

Now math is only an hobby for me (even if I don't study it at school I love it) so I tried again to solve this problem, using "new concept" I have "learnt" since I left school but still can't find a solution even using logarithm (aka even using a calculator).

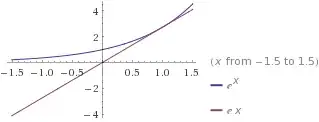
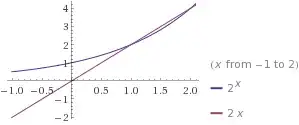
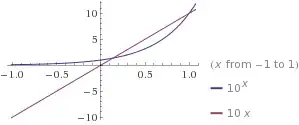
I noticed that $a^x-ax=0$ so I just need to find the zeros of the functions $f_a(x)=a^x-ax$ but I don't know how to solve this. My second attempt was to using a graphical method plotting $ax=y$ and $a^x=y$ and finding the intersection, but this doesn't satisfy me.

My last effort was to "unify" the two $x$'s and put them on the same side of the equation:

$$a^x=ax$$

$$\log_a(a^x)=\log_a(ax)$$

$$x=1+\log_a(x)$$

$$a^{x-1}=x$$

$$a=x^{1/(x-1)}$$

here I'm lost and I am starting to doubt that is possible to "bring" the $x$s using the "standard" algebra rules, to one side of the equation and get one $x$ "alone".

Maybe I need more powerful theoretic tools to face this problem, but I don't understand why I can't find a way to "reduce" it to a simple form with easy operations $(+,\cdot)$ and powers.

a) Maybe that means that the solution isn't even irrational? Why at this point all become harder?

b) How can I face this problem? How to find the solution? Which are the extra concepts I need? I accept complete answers (even if I wanted only hints because I love to solve problems on my own, but I think this is above my level)

I'm sorry for my terrible English but I'm using a translator. Thanks in advance.

Answer 1

We need to bring out a non-elementary (termed "special") function for this kind of problem; the one intended for this type of situation is the Lambert W function. It is defined to be the inverse function of $xe^x$ - that is, it satisfies the functional equation $W(x)e^{W(x)}=x$.

Now we wish to solve $ax=a^x$. Fix $a$, so that we're solving for $x$ in terms of $a$. Rearrange:

$$ax=e^{(\ln a)x}\iff xe^{-(\ln a)x}=a^{-1}\iff \color{Blue}{-(\ln a)x} e^{\color{Blue}{-(\ln a)x}}=\color{DarkGreen}{-(\ln a)/a}$$

$$\iff \color{Blue}{-(\ln a)x}=W\left(\color{DarkGreen}{-\frac{\ln a}{a}}\right)\iff x=-\frac{1}{\ln a}W\left(-\frac{\ln a}{a}\right).$$

Inverse functions can trip a lot of people up when they're new to the concept, and in particular, those that are inverse functions which are non-elementary (not able to be expressed with a finite number of the basic four operations combined with roots and powers and exponentials) can be pretty trick and take a bit of getting used to. The Lambert W function falls into this category occasionally, which is why I provide a full solution as an introduction on how to manipulate it.

Answer 2

No, the graphical approach is fastest and most easy. Here are three cases for a;

You can see there are 2 solutions for every a$\not=$e; a>0;

Even without much of graphing or solving, we can see that $x=1$ is a solution for each a. Now at $x=1$ , $ax$ will increase at a higher than $a^x$ . So, the straight line moves up the a^x curve. But at large $x$ this has to get reversed . So, there would be another solution for $x>1$

Answer 3

Assume $a \in \mathbb{R}^{+}\setminus\{1\}$ (trivial case: $1^{x}=1\cdot x$ iff $x=1$) and that solutions are sought in the reals.

Let $k=log(a)$ (which is well-defined and not equal to 0) and $y=kx$ and $\beta:=exp(k)/k$ which is $\neq 0$ and is positive resp. negative exactly when $k$ is positive resp. negative, exactly when $a>1$ resp. $0<a<1$

Then $a^{x}=a x \Leftrightarrow exp(y)-\beta y=0$.

Let $f : \mathbb{R}\to\mathbb{R} : x \mapsto exp(x)-\beta x$. Sought out is $x$ such that $f(x)=0$.

Case 1. $\beta>0$. One observes, that $f(x) > 0$ for $x\in(-\infty;0)$.

If there is a solution in $(0;\infty)$, then, since $f(0)=1>0$ and $f(\infty)=\infty$, there must exist a local minimum with function-value $\leq 0$; on the otherhand, if there be a local minimum with function-value $\leq 0$, then there is obviously a solution. Thus there is a solution in $(0;\infty)$ iff there is a critical point $x_{c} \in (0;\infty)$ with $f(x_{c})\leq 0$. Now $f´(x) = 0 \Leftrightarrow exp(x)-\beta=0 \Leftrightarrow x=log(\beta)$. So there is one critical point. This critical point is $>0$ iff $\beta>1$; the function-value is $f(log(\beta))=\beta-\beta log(\beta)$, which is $\leq 0$ iff $\beta\geq e$. Hence there is a solution in $(0;\infty)$ iff $\beta\geq e$.

Case 2. $\beta<0$. Now $f(-\infty)=-\infty$ and $f(0)=1>0$. Thus there is a solution $f(x)=0$ in $(-\infty;0)$.

Reasoning as in Case 1, there is a solution in $(0;\infty)$, exactly when $\beta\geq e$, which is not the case here, since $\beta<0$.

Conclusion. There is a solution exactly when $a<1$ or $a/log(a)\geq e$.

It can also be shown, that there be exactly one solution in case $a<1$ or $a/log(a)=e$, and exactly 2 in case $a/log(a)> e$.