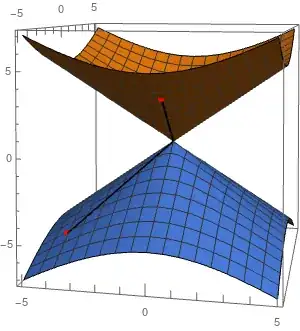
I want to show that the following subset of $\mathbb{R}^3$ is path connected. Define a double cone as below
$$M=\{(x,y,z)\in\mathbb{R}^3\mid x^2+y^2=z^2\}.$$
The only thing I know is the definition of path-connected. $M$ is path-connected if and only if for every two points $p_1,\,p_2\in M$ there is a continuous map $f:[t_1,t_2]\to M$ such that $f(t_1)=p_1$ and $f(t_2)=p_2$. I can intuitively say that $M$ is indeed path-connected by looking at $M$ in $\mathbb{R}^3$ which looks like below, but I don't how to right down a proof for it! Any help or hint is appreciated.