2

Find the inverse of: $F(x)=7x^5-5x^3-3x^2+2x$.

MGA
  • 9,636
Lance
  • 21
  • One does not invert equations. You can invert a function, though. Incidentally, this seems awfully difficult since the function is a 5th order polynomial. – Christopher A. Wong Apr 09 '13 at 00:42
  • Just wrap your equation in dollar signs, and voilà – The Chaz 2.0 Apr 09 '13 at 00:43
  • Thank you and I meant equation, I always seem to get those 2 words mixed around. I tried inversing it myself and could not get the correct function. – Lance Apr 09 '13 at 00:48
  • 3
    It is very unlikely that you were explicitly asked to do this. Perhaps you were asked to do something else $E$, and you knew that if you could find an explicit general formula for the inverse, you could do $E$. If one knew what $E$ was, perhaps one could suggest an alternative approach. – André Nicolas Apr 09 '13 at 00:49
  • What you are after is a solution to the equation $7x^5-5x^3-3x^2+2x-c=0$. This always has 5 solutions, but this particular function is not factorizable. – MGA Apr 09 '13 at 00:50
  • 1
    Please add why you want $f^{-1}$ ? Maybe there is any other approach to it. – ABC Apr 09 '13 at 00:55

3 Answers3

2

What you are given is a function $F(x)$, not an equation.

Start with $F(x) = y = 7x^5 - 5x^3 - 3x^2 + 2x$.

Exchange $x$ and $y$:

$x = 7y^5 - 5y^3 - 3y^2 + 2y= y(7y^4 - 5 y^2 - 3y + 2)$ and "solve" for $y$ to express it in terms of $x$, but rename $y$ as $y^*$ to avoid confusion with the rest of the description of the most frequent technique for finding the inverse of a function, in general.

(In this case, this will not be terribly easy, algebraically!)

Then $F^{-1}(x) = y^*$

I just saw your comment: is this the approach you tried?

amWhy
  • 209,954
2

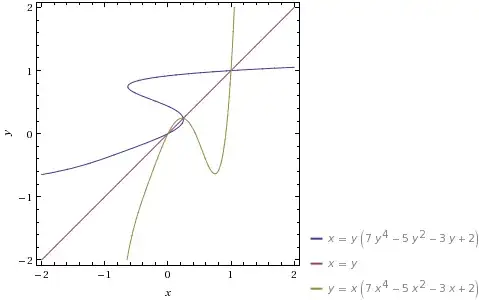
enter image description here

$f(x),x,f^{-1}(x)$ in same plot. Maybe this can help if you want to see behavior of curves or find number of intersections.

ABC
  • 6,034
0

If you use Mathematica, here's what I'd do:

Make a table of small increments

mytable = Table[{ f [x] , x } , {x, 0, 10, 0.01} ]

Then you can plot this and get a visual representation of the inverse. If you want the analytical inverse, just use the Fit function on this table to get a polynomial like this:

myfit = Fit[mytable, {1, x, x^2, x^3, x^4}, x]

This will at least get you a polynomial function that is the inverse, though it won't be the true inverse, just an approximation.

Sarah
  • 1