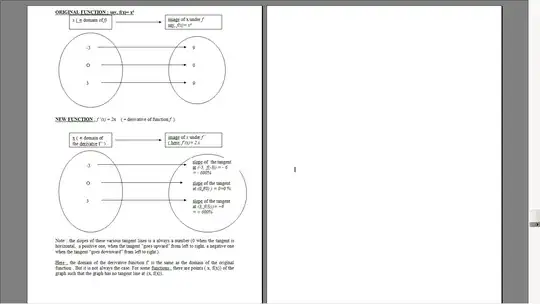
- The formula defining the derivative function is not itself the equation of the tangent; this formula gives you , for each tangent ( one tangent for each point $(x, f(x))$ of the graph of $f$ ), the slope of this line. And a slope is a number.
The main point here is that the derivative function is a function that sends back numbers as outputs ( not lines, not tangents). One and only one number far every permissible input $x$.
- To understand this, remember that for all point $(x, f(x))$ of the graph (such that there is a tangent to the graph at this point), this tangent will have the form :
$$y = mx + b$$.
The number $m$ is the slope of the tangent. You may think of it as a percent ( in the same way as we ordinarily think of the slope of a road in terms of %).
For example, the slope of the line $y = 0,5x +2$ has slope $0,5$, that is, $50$%. The slope of the line $6x + 10$ has slope $6$, that is $600$%. The slope of $y=0x+5=5$ is $O$ ( = $0$%). The slope of $y= -2x +40$ is $-2$ = $- 200$% ( These are arbitrary examples, not related to the $x^3$ function).
So, for each input $x$, the derivative gives as output the number $m$ ( that is, the slope) of the tangent to the graph at point $( x, f(x))$.
The beauty is that, although the tangents will ( ordinarily) have various slopes, although the outputs of function $f'(x)$ will be different for different $x$ values ( inputs), we are often able to find a rule defining a constant numerical relation between the value of $x$ and the corresponding slope. For example, for $f(x)=x²$, it can be proved that $f'(x)$ ( the slope of the tangent to the graph of $f$ at $(x, f(x))$) is always the double of x ! This is what means the differentiation rule : $\frac {d} {dx}x^2$ $=$ $2\times x$.
Note : this number that is sent back as output is formally defined as a limit, namely, the limit , as $h$ approaches $0$ , of the ratio
$\frac {f(x+h) - f(x)} { (x+h) - x}$ = $\frac{change- in-y}{change-in-x}$
This shows that the slope of the tangent happens to be identical to the instantaneous rate of growth of the original function $f$ at the point $( x, f(x))$. This is why, in fact, we are interested in these slopes.
Note : you can use the number $f'(a)$ to find the equation of the tangent at a given point $( a, f(a))$. Since $f'(a)$ is " the $m$ ( = slope) of this tangent" ,the equation of this line will have the form : $y = f'(a)x + b$. The fact that you also know one point of this tangent , namely, the point $(a, f(a))$, allows you ( with some algebra) to recover the number $b$ , and finally the whole equation of the tangent at this point $( a, f(a))$.
- Examples with $f(x)= x^3$ and consequently $f'(x)= 3x^2$:
For $x= 1$ , the slope is $f'(1)$ = $3\times1^2$= $3$ = $300$%
So, at $( 1, f(1))$ , the slope of the tangent to the graph of $f$ is $300$%. Quite a big slope.
For $x= 2$ , the slope is $f'(2)$=$3\times2^2$= 12 = $1200$%
So, at $( 3, f(3))$ , the slope of the tangent to the graph of $f$ is $1200$%. A huge slope!