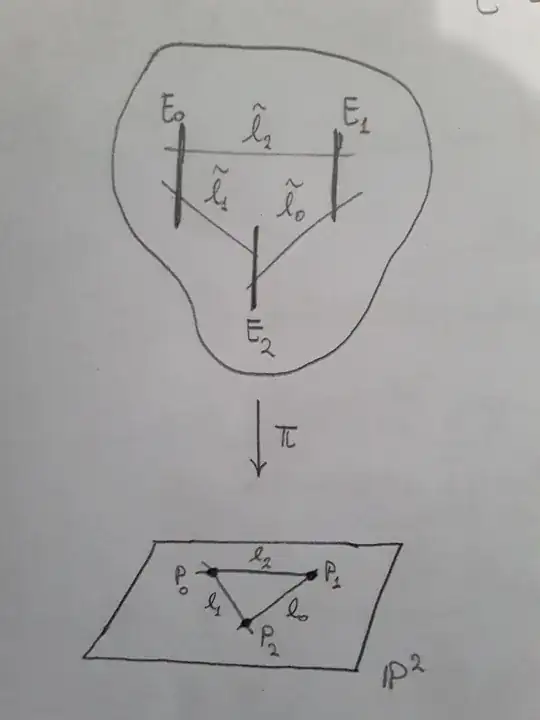
Let $P_0,P_1,P_2\in\Bbb{P}^2$ points in general position,consider the lines $\ell_i:=\overline{P_jP_k}$ for $\{i,j,k\}=\{0,1,2\}$ and the blow-up $\pi:S\to\mathbb{P}^2$ at $P_0,P_1,P_2$.
I was told in that the strict transform $\widetilde{\ell}_i\subset S$ of $\ell_i$ is supposed to have self-intersection $-1$, and that we may then apply Castelnuovo's contraction theorem successively to each curve $\widetilde{\ell}_0,\widetilde{\ell}_1,\widetilde{\ell}_2$.
I can't see why it should be $-1$. Take for example $\ell_2=\overline{P_0P_1}$, which has self intersection $0$. Now, since $\ell_2$ passes through both $P_0,P_1$ with multiplicity $1$, then:
\begin{align*} 0&=\ell_2^2\\ &=(\pi^*\ell_2)^2\\ &=(\widetilde{\ell}_2+E_0+E_1)^2\\ &=\widetilde{\ell}_2^2+E_0^2+E_1^2+2\widetilde{\ell}_2E_0+2\widetilde{\ell}_2E_1+2E_0E_1\\ &=\widetilde{\ell}_2^2-1-1+2+2+0 \end{align*}
Therefore $\widetilde{\ell}_2^2=-2$. Analogously, I've found $\widetilde{\ell}_0^2=\widetilde{\ell}_1^2=-2$.
What am I missing here?