1

Let $A,B$ and $C$ be independent random variables, uniformly distributed over $[0,5], [0,1]$ and $[0,2]$ respectively. What is the probability that both roots of the equation $Ax^2+Bx+C=0$ are real?

I know I have to do triple integral. Here are steps, as suggested in comment.

  1. Write an integral of uniform probability density over entire space of possible combinations. In this case, the "box" is rectangular and so integral bounds are trivial.
  2. Find a defining equation for your condition to hold (discriminant, in our case)
  3. Change integral boundaries so that you only integrate over portion where the condition is true

I am struggling in Step-3

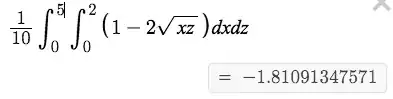
enter image description here

Rohit Singh
  • 1,143
Tai Heng Liu
  • 11
  • Try to solve it yourself, but here's how you normally start in these cases:
    1. write an integral of uniform probability density over entire space of possible combinations (this just gives you 1). In this case, the "box" is rectangular and so integral bounds are trivial.
    2. find a defining equation for your condition to hold (discriminant, in our case)
    3. change integral boundaries so that you only integrate over portion where the condition is true
     – orion Feb 13 '20 at 09:08
  • @orion Step 3 is part I am struggling with. – Tai Heng Liu Feb 13 '20 at 09:15
  • Just to make some connections: 29242 is the node for the basic version with all three uniforms being in $[0,1]$. There are similar questions where the ranges of the unifs differ: 3182777, 1528677, and 877374. – Lee David Chung Lin Feb 13 '20 at 09:19
  • I know the rectangular is has area of 10. My discriminant is B^2-4ac is greater than 0. – Tai Heng Liu Feb 13 '20 at 09:20
  • @LeeDavidChungLin Thank you for finding a similar problem but I am have terrible with a question. – Tai Heng Liu Feb 13 '20 at 09:24
  • if I can't figure it out, I ask my professor Friday when I see him. – Tai Heng Liu Feb 13 '20 at 09:28

2 Answers2

2

Following Polya's advice let's break this down into steps and then solve each step:

  • How do we know if the roots of $ax^2 + bx + c=0$ are real ? The roots are real if the discriminant $b^2-4ac$ is greater than or equal to $0$.
  • We are told $a,b,c$ are uniformly distributed within the cuboid region $0 \le a \le 5; 0\le b \le 1; 0 \le c \le 2$. So we can re-state the problem as "in what proportion of the cuboid is $b^2-4ac \ge 0$ ?".
  • We know that the volume of the cuboid is $10$. So we need to find the volume of the cuboid in which $b^2-4ac \ge0$ and then divide this by $10$.
  • Let's consider a simpler two-dimensional problem. Suppose $c$ is fixed at some value $C$ (so we are taking a slice of the cuboid). In what area within the rectangle $0 \le a \le 5; 0\le b \le 1$ is $b^2-4aC \ge 0$ ?
  • We can re-state this again. For a fixed value $C$, in what area within the rectangle $0 \le a \le 5; 0\le b \le 1$ is $\displaystyle a \le \frac {b^2} {4C}$ ?

  • Sketch a diagram. From the sketch it becomes clear that we need to find the area $A$ between the curve $\displaystyle a = \max (\frac {b^2} {4C}, 5)$ and the line $a=0$ that is also between the lines $b=0$ and $b=1$. We can do find by integration:

    $\displaystyle A(C) = \int_0^1 \max (\frac {b^2} {4C}, 5) db$

  • This gives us the area $A(C)$ for a slice $c=C$ of the cuboid. To find the volume across the whole cuboid we have to integrate $A(c)$ between $c=0$ and $c=2$. Then divide by 10 to find the answer to the original problem.

gandalf61
  • 15,326
1

You start with this: given a quadratic equation, how can you tell whether both roots are real? There is (a part of) a very well-known formula you can use.

Once you have that, you see that this condition will describe part of the box defined by the domains of $A,B,C$. Find the volume of that part, and you're very nearly done.

Arthur
  • 199,419
  • 1
    oh, use the discriminant – user29418 Feb 13 '20 at 08:23
  • B^2-4ac is great than 0 – Tai Heng Liu Feb 13 '20 at 08:24
  • what are discriminant ? – Tai Heng Liu Feb 13 '20 at 08:25
  • @TaiHengLiu That is the discriminant. $B^2-4AC$. It "discriminates" (tells the difference) between equations with real solutions and equations with non-real solutions, hence the name. – Arthur Feb 13 '20 at 08:31
  • okay but how would I set up integral, because i keep getting -1.81 as my answer. I know the probability is [0,1]. It's been struggling to answer this question. – Tai Heng Liu Feb 13 '20 at 08:33
  • @TaiHengLiu Well, you're integrating the function $1$ over a region. That really ought to give you a positive answer. Are you certain that all the bounds are in the right order? And remember that the entire box has a volume $10$, yet the probability of being inside it is $1$. – Arthur Feb 13 '20 at 08:34
  • I have never learned a triple integral. either or double integral. Also its the lead coefficient 1/10 . – Tai Heng Liu Feb 13 '20 at 08:35
  • @TaiHengLiu If you don't know how to set up triple integrals, this really isn't the best problem to practice on. I have to work soon, so I can't really write a repeated integral guide right now. Consider doing some simpler, purely integration exercises first, to get the hang of it. Then come back to this exercise once you know how to set up a repeated integral like this. – Arthur Feb 13 '20 at 08:38
  • It's a question from my homework. I am just trying to get a perfect on the homework. – Tai Heng Liu Feb 13 '20 at 08:40
  • 1
    @TaiHengLiu Then copying someone else's triple integrals without actually knowing how they work might get you a better score for this one homework, but it won't help you get better at this. What about next homework? Are you going to be helpless there too? What about your exams? If you don't know how to do this, and your class expects you to, you really ought to practice. – Arthur Feb 13 '20 at 08:41
  • I took the class because the pre-req stated only need up to accelerated calc 2. In our school even accelerated calc 2 never teaches triple integral. – Tai Heng Liu Feb 13 '20 at 08:43
  • @Arthur, I would not be taking if I did not meet the pre-req for this course. I know a decent amount of my class has only experienced a single integral. It's Math 372 from the University of Hawaii at Manoa. – Tai Heng Liu Feb 13 '20 at 08:51