0

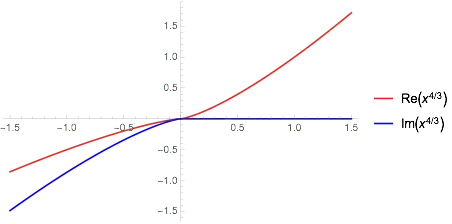
I was trying to plot the graph of $y=x^\frac{4}{3}$. However, I tried two online plotters, both gave me curves only on the right side of the y-axis. There is nothing on the left side of the y-axis. Shouldn't it be a curve symmetric to the y-axis? Similarily for $y=x^\frac{5}{3}$ which I thought is a function symmetric to origin but only has value for nonnegative x.

I tried to use google to compute $(-1)^\frac{4}{3}$ and it automatically gives me $-0.5 - 0.866025404 i$ instead of $1$. And $(-1)^\frac{5}{3}$ got a answer of $0.5 - 0.866025404 i$ instead of $-1$. Why does the result include an imaginary part?

cs_snake
  • 3

3 Answers3

1

Fractional powers of negative numbers aren't uniquely defined.

There are three cube roots of $-1$: $-1$, $\frac12+\frac{\sqrt{3}}2i$, and $\frac12-\frac{\sqrt3}2i$.

The answer given by Google for $(-1)^{4/3}$ was the fourth power of the middle one of those three.

J. W. Tanner
  • 60,406
  • In my opinion, this is a flaw in Wolfram Alpha: if $q$ is odd, the principal root of $x^{p/q}$ should be real. But others will no doubt disagree. – TonyK Feb 11 '20 at 20:45
  • cf. principal value – J. W. Tanner Feb 11 '20 at 20:47
  • Wolfram Alpha gives also the function $cbrt$ for the real value cube root : https://www.wolframalpha.com/input/?i=plot+cbrt++x%5E4 – Emilio Novati Feb 11 '20 at 20:48
  • 2
    It isn't unheard of to attempt to uniquely define arbitrary powers (including fractional) for arbitrary bases. For example here as $(-1)^{\frac{4}{3}}=e^{\text{Ln}((-1)^{\frac{4}{3}})}=e^{\frac{4}{3}\text{Ln}(-1)}$, noting here that $\text{Ln}$ is in reference to the Principal logarithm. In doing so, however, the function fails to be analytic or continuous in several places due to branch cuts, and there are different practices in terms of where to place the branch cut in the first place. – JMoravitz Feb 11 '20 at 20:50
0

$$\displaystyle (-1)^{4/3}=\left[e^{(2k-1)\pi i}\right]^{4/3}, \quad k\in \{0,1,2\}$$

$$\displaystyle (-1)^{4/3} \in \left\{ e^{-\frac{4\pi i}{3}}, e^\frac{4\pi i}{3}, e^{4\pi i} \right\}$$

We can write this in rectangular coordinates:

$$\displaystyle (-1)^{4/3} \in \left\{- \frac{1}{2}+\frac{\sqrt{3}}{2}, -\frac{1}{2}-\frac{\sqrt{3}}{2}, 1 \right\}$$

mjw
  • 8,647
  • 1
  • 8
  • 23
-3

The function is defined for positive and negative values of $x$. The graph shows the real and imaginary parts:

Mathematica plot

$${\rm Re}[(-1)^{4/3}] = -\frac{1}{2}$$

$${\rm Im}[(-1)^{4/3}] = - \frac{\sqrt{3}}{2}$$

Given that there is no unique way to compute a partial root of a negative number, Mathematica seems to assume the most general complex form.

There is no reason that the function should be (or is) symmetric with respect to the interchange $x \leftrightarrow -x$.

David G. Stork
  • 29,774