1

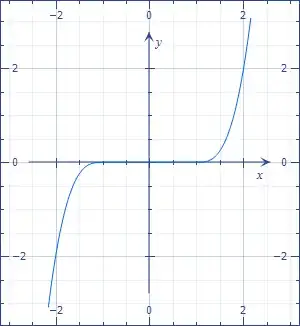
When solving separable differential equations we divide both sides of the equation by the part containing our function y. When dividing, we have to separately check the case when we would divide by zero. For example: $$y' = 3y^{2/3}$$ $$\int y^{-2/3}dy = \int 3dx$$ $$y^{1/3} = x + C$$ $$y = (x+C)^3$$ This is the general solution. We also have to check the case of $y^{2/3} = 0 \Rightarrow y' = 0$. Function $y(x) = 0$ is a separate solution.

The question is why can't there be a solution where $y=0$ only for a few values of x, but not for all of them? Why do we only check the constant zero function?

I have read some similar questions on this topic and usually the answer is that for every point on the xy plane there is only one solution through this point. But I don't understand why that is true for every differential equation, for example for this one?

Binabik
  • 63

1 Answers1

2

You are quite right.

Any solution coming from the negative $y$'s, then reaching $0$, staying on $0$ for a while and finally leaving to the positive $y$ is a solution:

  • it is everywhere differentiable,

  • it fulfills the differential equation.

enter image description here

You can also have just the negative or positive tail.

In fact, you are not "allowed" to integrate across the singular point, so that $y=(x+c)^3$ does not need to hold everywhere.

  • Sorry, what do you mean by "you are not "allowed" to integrate across the singular point, so that $y=(x+c)^3$ does not need to hold everywhere"? – Binabik Feb 10 '20 at 13:59
  • Re-read your solution. It is based on a possibly improper integral. –  Feb 10 '20 at 14:01