The question is from JEE Advanced(2017), where it asks to identify matrices which are the square of a matrix with real entries:
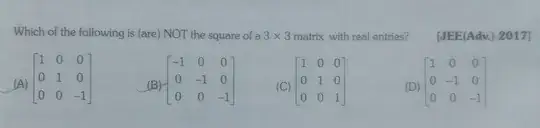I first found out the determinant of all the matrices. Options (A & B) both have negative determinant value and hence can't be expressed as square of a matrix with real entries. For explanation let any of the two be called as $A$ . Given they are square of another matrix(let $B$) so $B^2=A$ . Taking the determinant on both sides, I get $|B|^2=|A|$ and since $|A|$ is negative, I get $|B|^2<0$. So $B$ can't have all real entries. Option C is $I$ whose square is $I$ or vice versa. I am having trouble with option D . Since it's determinant is also positive and I can't find a simple matrix which when squared gives that option. I have talked to my teacher . He said there is a method to find square root of a matrix but that's far beyond our level. I am a High school student studying in grade 12. So please, if possible, give a simplified hint/answer.
Thanks in advance!
Asked
Active
Viewed 815 times
3
Firefox1921
- 69
Harsh jain
- 286
2 Answers
2
The determinant of a $3\times 3$ matrix being positive is a necessary and sufficient condition for it to have atleast one real root.
Sam
- 2,447
-
I don't think so. Can you prove it or provide any reference – Harsh jain Feb 10 '20 at 02:04
-
The proof is here. I assumed that you would not understand the high-level math in it. – Sam Feb 10 '20 at 08:52
0
Regarding only the $yz$ plane, $D$ rotates by 180°. What if you rotate by 90° twice?
Hagen von Eitzen
- 374,180
-
von I don't understand what you're trying to say . They represent planes if combined with x,y,z. But it's only numerical matrix – Harsh jain Feb 10 '20 at 02:05