This question has been bugging me ever since my multivariable calculus class. I know that gradient is the direction of steepest ascent( Since dot product gives directional derivative and for cos$\theta$ to be maximum, along the direction of gradient). I've also seen it used as a normal, whenever we want to find the tangent planes or anything.
What confuses me is, how does it make sense for it to be both? Did I understand/interpret it wrong?
Let's consider the situation in $2D$ --- our humble line equation uses a function $f(x, y) \equiv ax + by$, and our line is defined by the solution set $L \equiv \{ (x, y) : f(x, y) = 0 \}$. (For now, let's stick to lines passing through the origin).
If we now consider the gradient, we get
$$ n \equiv \nabla f \equiv \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right) = (a, b) $$
I denote the gradient by $n \equiv (a, b)$ (for normal), since I'm going to rewrite $f$ as follows:
$$ f: \mathbb R \times \mathbb R \rightarrow \mathbb R \qquad f(x, y) = ax + by = (a, b)^T(x, y) $$
If I now write $f$ as a function that recieves one argument $p \in \mathbb R^2$, I can write the above equation as:
$$ f: \mathbb R^2 \rightarrow \mathbb R \qquad f(p) = n^T p $$
Our line is defined by $L \equiv \{ p \in \mathbb R^2 : f(p) = 0 \}$, which means that we want to find those directions p which are orthogonal to n. This (algebraically) tells us why the gradient allows us to find the normal.
Now a particular example: $x + y = 0$:
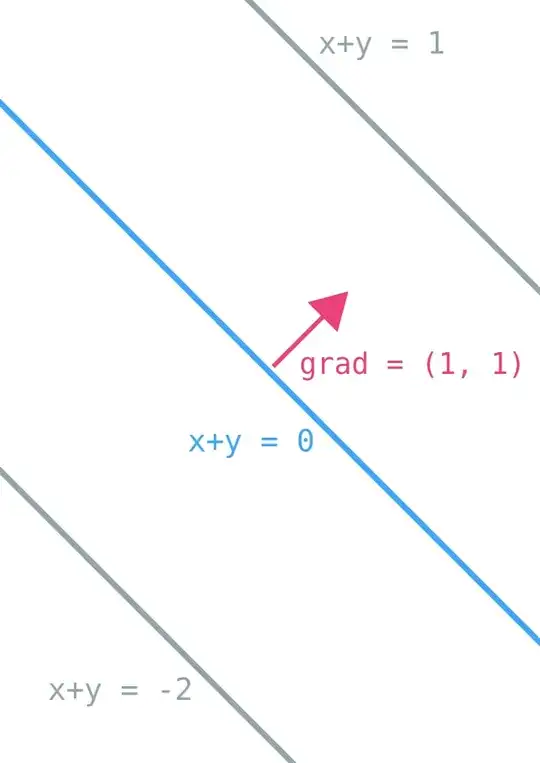
The gradient points in the direction where the quantity $x + y$ increases. What we're interested is in all those points where $x + y = \texttt{constant}$. So:
