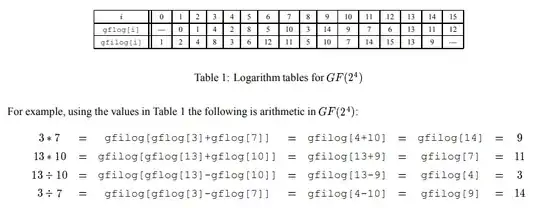
I've followed this tutorial (http://web.eecs.utk.edu/~jplank/plank/papers/CS-96-332.pdf) which introduces Reed-Solomon coding and therefore covers finite fields. My problem is with one of the examples of how the logarithm and anti logarithm tables are looked up to perform a division. I have included an image of the examples and table below:
The tutorial is written for programmers and so $gflog[i]$ is really $log_2(i)$ and $gfilog[i]$ is $log_2^{-1}(i)$.
I am able to follow all but the last example. I used an online finite field calculator which indicates the result should be $10$. The result in the example is $14$, at first I assume this to be a simple mistake of looking up the result in the incorrect row (i.e, looking up the $log_2(i)$ row instead of the $log_2^{-1}(i)$ row) as the table correctly shows the result should be $10$.
But upon closer inspection, their arithmetic for the indexing into the table seems to be off for the final example, $gfilog[4-10] = gfilog[9]$. Shouldn't the result be $gfilog[10]$?
Now my what I suspect is happening is the arithmetic on the indexes is regular integer arithmetic. And in this case, $4-10$ results in $-6$. Since this is an invalid index, and the log tables are over $GF(2^4)$, the correct position of $-6$ is determined by $-6 mod 16$ which gives $10$. However! the $10$ is just the rank of the correct index and not the index itself. Therefore, the 10th position on the table is really at the 9th index. Hence $gfilog[9] = 10$.
Is my understanding of this correct? I've tried this out with a few other values and it seems to work out. This is all very new to me, so kindly elaborate a bit in your responses as my background is primarily in programming :)