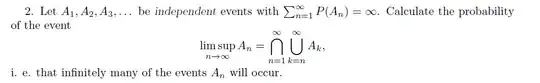1

enter image description here

I tried to do this problem using Borel-Canteli lemma and got answer as 1, but my professor said its incorrect. His comments are below:

"This problem has nothing to do with the Borel-Cantelli Lemma! The condition of that lemma is just the opposite of what we have here, that is, its condition is that the sum of the probabilities of A_n is FINITE. Incidentally, your answer is correct, but the explanation is wrong."

He suggested: "Use the complementer event, and try to calculate the probability of the even that NO A_n occurs for all n>N with as give threshold N. Use the independence."

I am having a hard time understanding this or getting this part. Can someone please help me on this?

Let me know if you have concerns or questions.

Math_Is_Fun
  • 692
  • "Has nothing to do" is a bit stretching. The claim of the probelm statement is also known as the second Borel-Cantelli lemma (though it is due to Erdös-Rényi). How about you tell us how you applied Borel-Cantelli to the problem at hand? – Hagen von Eitzen Feb 04 '20 at 04:57
  • I am super confused with this, I used Borel-Cantelli lemma in this way: If, sum of probabilities of (An) is equal to infinity, then the probability of the event is lim (sup (An)), where n tends to infinity = 1, and if the sum is < infinity, then the result will be 0. Since, in the question its stated that it is equal to infinity, therefore our answer is 1. That's it... – Math_Is_Fun Feb 04 '20 at 06:32
  • Have you looked at the Wikipedia article on the Borel–Cantelli lemma? Are you aware that it discusses the converse? – joriki Feb 04 '20 at 07:06
  • No im sorry I didnt. Now I looked up on the internet and found few pdfs on this topic from some universities and found the answer. I think I can formulate and write it correctly. It should work, thanks a lot sir. – Math_Is_Fun Feb 04 '20 at 07:10
  • I think this will also give me a pretty good idea about what I am supposed to do to solve these kind of problems. https://math.stackexchange.com/questions/2833047/proof-of-the-converse-borel-cantelli-lemma?rq=1 – Math_Is_Fun Feb 04 '20 at 07:12
  • @Math_Is_Fun: Then you could post your answer here and accept it so that your question doesn't remain unanswered. – joriki Feb 04 '20 at 08:30
  • Sure sir, I will. :) – Math_Is_Fun Feb 05 '20 at 03:20

0 Answers0