Intuitive idea of the Lipschitz function

Question

I'm trying to understand intuitively the notion of Lipschitz function.

I can't understand why bounded function doesn't imply Lipschitz function.
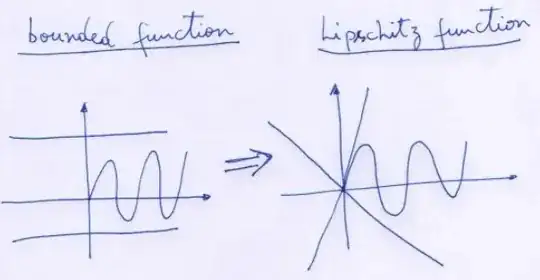
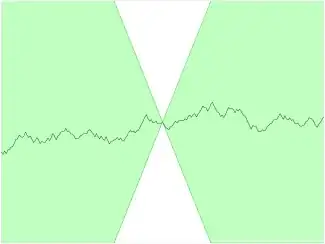
enter image description here

I need a counterexample or an intuitive idea to clarify my notion of Lipschitz function.

I need help

Thanks a lot

score 75 · Answer 1 · edited Feb 16 '14 at 09:59

75

A Lipschitz function is such that $$|f(x)-f(y)|\leq \alpha |x-y|$$ for any points you pick. Writing this as $$\left|\frac{f(x)-f(y)}{x-y} \right|\leq \alpha $$

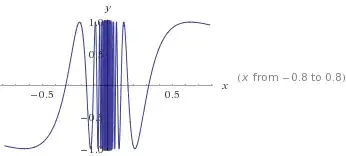
what we're saying is that the slope of the secant line joining $(x,f(x))$ and $(y,f(y))$ is always bounded above by $\alpha$. An example of a Lipschitz function is $\sin x$, or $x$. An example of a function which is not Lipschitz but is bounded is $$\sin (x^2)$$ over $\Bbb R$. This is because as we go further towards $+\infty$, the oscillation becomes faster, and thus the slope of the secant lines get nearer and nearer to vertical ones.

An example of a function that is not Lipschitz nor bounded is $\sqrt x$ over $\Bbb R_{>0}$. This is because if we fix $x=0$ and make $y$ very close to $0$, the slope of the secant line grows without bound.

Finally, we can give an example of a function which is Lipschitz but isn't bounded: $x+\sin x$ over $\Bbb R$. Its slope will never get larger than $1$.

edited Feb 16 '14 at 09:59

answered Apr 06 '13 at 20:30

Pedro

122,002

1

Excellent explanation! +1 – Clayton Apr 06 '13 at 20:33
If a function has a derivative that is bounded, must it be a Lipschitz function? – Peter Olson Apr 07 '13 at 00:28
@PeterOlson Assume $f$ has bounded derivative. By the Mean Value Theorem, for each $x,y\in\operatorname{dom}f$, what can you equate $$\frac{f(x)-f(y)}{x-y}$$ to? – Pedro Apr 07 '13 at 00:34
In case of root x, near zero, isn't the slope becoming zero? Can we still say the slope is increasing without bound? ( though I know it is not lipschitz, only trying to understand it intuitively). – aarbee Nov 03 '16 at 06:01
Hi Pedro Tamaroff, can you guide us with the next please https://math.stackexchange.com/questions/2440926/measurable-functions-and-existence-decreasing-function – mathd Sep 25 '17 at 05:04
Is Lipschitz continuity then actually the same as $|df(x)/dx| < a$? – asmaier Nov 29 '17 at 16:07
@asmaier I don't think a bounded first derivative is the same as the Lipschitz condition. 1. The Lipschitz condition does not require differentiability, 2. the Lipschitz condition requires every secant line to have a bounded slope whereas a bounded derivative corresponds to every tangent line having a bounded slope. – fool Jun 15 '23 at 19:11
@user But maybe the other way round: Every function with a bounded first derivative is also a Lipschitz function? – asmaier Jun 16 '23 at 15:51
1

@asmaier I think you're correct! See https://math.stackexchange.com/questions/1165431/is-a-function-lipschitz-if-and-only-if-its-derivative-is-bounded – fool Jun 17 '23 at 01:44

vonjd · Accepted Answer · 2015-06-16T16:41:10.123

44

It means that your function does not explode at some point - made mathematically rigorous.

This idea can also be shown geometrically like so (picture from wikipedia):

enter image description here

The Lipschitz condition (or Lipschitz continuity) ensures that your function always remains entirely outside the white cone, so it cannot e.g. become infinitely steep at one point.

Concerning your picture: Think of the function $sin(1/x)$ (source W|A):

enter image description here

You see that it is becoming infinitely steep at the origin (and would therefore run into the white cone!) but it is still bounded.

This condition is e.g. used in the theory of differential equations where it guarantees the existence and uniqueness of solutions to certain types of differential equations.

edited Jun 16 '15 at 16:41

answered Jun 16 '15 at 13:46

vonjd

8,810

yes, but in every bounded function I can draw this kind of cone (see the picture of my question). – user42912 Jun 16 '15 at 13:50
@user42912: No, you cannot: See my edit for clarification. – vonjd Jun 16 '15 at 14:18
@user42912: Does this help you? – vonjd Jun 16 '15 at 16:40
1

yes, now I got it! thank you very much! – user42912 Jun 16 '15 at 17:09
It's a nice way of thinking. Thanks. But I am not able to relate root x with this line of thinking. Any help pls? – aarbee Oct 29 '16 at 05:09
@Ramit $\sqrt{x}$ is not Lipschitz. – Idonknow May 15 '18 at 23:14

score 7 · Answer 3 · answered Apr 06 '13 at 20:22

7

Look at the square root function on $[0,1]$ and its behaviour at 0.

answered Apr 06 '13 at 20:22

ncmathsadist

49,383

score 2 · Answer 4 · answered Apr 06 '13 at 20:24

2

Look at the unitary circle, $f(x)=\sqrt{1-x^2}$ how is the tangent line in $x=1$?

answered Apr 06 '13 at 20:24

Gaston Burrull

5,449
5
33
78

Halil Duru · Answer 5 · 2013-04-06T21:20:29.387

0

With this version (just assuming boundedness) , any discontinuous bounded function forms a counter-example .[why?]

But if you also assume continuity , see the examples below/above.

Furthermore , you may even have differentiability and boundedness without Lipschitzness......

edited Apr 06 '13 at 21:20

answered Apr 06 '13 at 20:34

Halil Duru

1,347

How could a function be differentiable without being lipschitz? – treble Apr 06 '13 at 21:01
Look at Tamaroff's example $sin[x^2]$ ..Isn't it differentiable? – Halil Duru Apr 06 '13 at 21:19
OK, I wasn't thinking about the derivative going to infinity. – treble Apr 06 '13 at 22:28

Intuitive idea of the Lipschitz function

5 Answers5

Linked

Related