Let $X$ and $Y$ be topological spaces, and let $A\subseteq X$ and $B\subseteq Y$ be subsets. Then we naturally give $A$ and $B$ the (subspace) topologies induced by the inclusion maps $$i : A\hookrightarrow X\qquad\qquad\text{and}\qquad\qquad j : B\hookrightarrow Y.$$
What about the product $A\times B$? There are two natural options for topologizing $A\times B$, namely:
- $A\times B$ is the product of the spaces $A$ and $B$, so you give it the product topology
- first give $X\times Y$ the product topology and then observe that the underlying set of $A\times B$ is a subset of $X\times Y$, so it makes sense to give $A\times B$ the (subspace) topology induced by the inclusion map $k : A\times B\to X\times Y$.
Are these two topologies on $A\times B$ the same?
My trial:
My steps is to describe:
the first topology given
1- (the first topology given)The product $A \times B$ by the universal property:
where $\exists ! t_{1} = (f_{1}, g_{1})$ that makes the diagram commutes.
and the set-world product $A\times B$ of their underlying sets is a topology world product iff it is given a unique largest topology for which a map $t_{1} : T_{1} \rightarrow A\times B$ is continuous iff $Pr_{A} \circ t_{1}$ and $Pr_{B} \circ t_{1}$ are both continuous.
And the open sets are sets of the form $U_{1} \times V_{1}$ where $U_{1} \subseteq A$ is open in $A$ and $V_{1} \subseteq B$ is open in $B.$
2-(the second topology given in 2 steps )
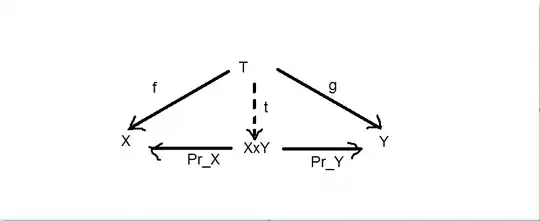
a- The product $X \times Y$ by the universal property:
where $\exists ! t = (f, g)$ that makes the diagram commutes.
and the set-world product $X\times Y$ of their underlying sets is a topology world product iff it is given a unique largest topology for which a map $t : T \rightarrow X\times Y$ is continuous iff $Pr_{X} \circ t$ and $Pr_{Y} \circ t$ are both continuous.
And the open sets are sets of the form $U \times V$ where $U \subseteq A$ is open in $A$ and $V \subseteq B$ is open in $B.$
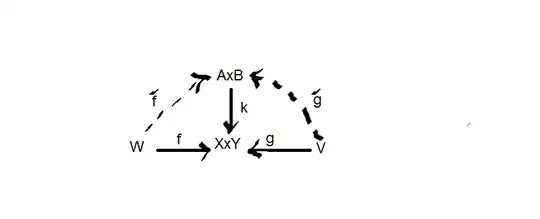
b- describing the subspace topology on $A \times B$ if it is considered as a subset of $X\times Y$ through the inclusion map $k$ by the following universal property:
such that the diagram commutes i.e. $k \circ \tilde{f} = f$ and $k \circ \tilde{g} = g.$
where $A\times B$ is a subset of $X \times Y,$ so it makes sense to give $A\times B$ the unique smallest subspace topology induced by the inclusion map $k.$
My questions are:
1- I know that those two topologies should be equivalent by 5.4(pg.90) in Munkres first edition by the hint given to me here Are these 2 topologies equivalent? but I do not know how to draw the universal property(especially because I am not sure that my drawing for the universal property of $A\times B$ as a subset of $X \times Y,$ is correct ) in case of the second topology to show its equivalence with the first topology, could anyone help me in solving this problem please?
2- Also, I am unable to describe the open sets in the case of the second topology and how they are the same as those in the first topology (I am assuming that the hint given in the other question is the form of the open sets but I do not know how), could anyone help me in this please?