$ \newcommand{\d}[1]{\, \mathrm{d} #1} \newcommand{\sgn}{\mathrm{sgn}} $ Let $f \in C[0,1]$. I am trying to show that: $$ \sup_{g \in C[0,1], \|g\|_\infty = 1} \left|\int_0^1 f(x)g(x) \d{x}\right| = \int_0^1 |f(x)| \d{x} $$ Here, $\|g\|_\infty := \sup_{x \in [0,1]} |g(x)|$ denotes the sup norm. Note that I'm not certain if this statement is true, but I strongly believe it's true.
If we remove the restriction that $g$ is continuous, then this statement is trivial, as we can simply let $g = \sgn \circ f$. Then $f(x)g(x) = |f(x)|$ $\forall x \in [0,1]$. To adhere to the restriction, my idea is to construct a sequence of functions $g_n$ such that as $n \to \infty$, $g_n$ "looks more and more similar" to $\sgn \circ f$. The following is an illustration of my idea:
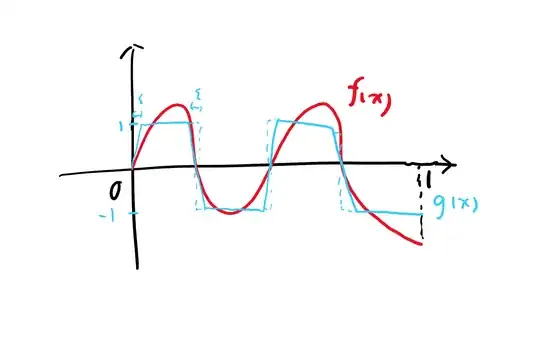As one can see, $g$ behaves similar to $\sgn \circ f$, but when it is $\epsilon$ away from a zero point, it connects to the zero point linearly so to make it continuous. It's also clear that $\|g_n\|_\infty = 1$, unless $f \equiv 0$, in which then it is a trivial case. My idea is to let $\epsilon = \frac{1}{n}$, for each $g_n$, and show that:
$$
\lim_{n \to \infty} \int_0^1 f(x)g_n(x) \d{x} = \int_0^1 |f(x)| \d{x}
$$
The following is my attempt to formulate a rigorous construction of $g_n$:
Define: $$ X_0 := \{x \in [0,1] : f(x) = 0\} $$ For each $x \in [0,1]$, define: $$ z_+(x) = \inf((x,1] \cap X_0) \\ z_-(x) = \sup([0,x) \cap X_0) $$ And finally, for each $\epsilon > 0$, define $h_\epsilon$ as follows: $$ h_\epsilon(x) = \begin{cases} 0, &\text{if $|z_+(x) - z_-(x)| \leq 2\epsilon$ or $x = 0$} \\ \frac{1}{\epsilon}(x - z_-(x)), &\text{if $|z_+(x) - z_-(x)| \leq 2\epsilon$ and $x < z_-(x) + \epsilon$ and $x > 0$} \\ -\frac{1}{\epsilon}(x - z_+(x)), &\text{if $|z_+(x) - z_-(x)| \leq 2\epsilon$ and $x > z_+(x) + \epsilon$ and $x > 0$} \\ -\frac{1}{\epsilon}(x - z_-(x)), &\text{if $|z_+(x) - z_-(x)| \leq 2\epsilon$ and $x < z_-(x) + \epsilon$ and $x < 0$} \\ \frac{1}{\epsilon}(x - z_+(x)), &\text{if $|z_+(x) - z_-(x)| \leq 2\epsilon$ and $x > z_+(x) + \epsilon$ and $x < 0$} \\ 1, &\text{if none of the above and $x > 0$} \\ -1, &\text{otherwise} \end{cases} $$ We then denote $g_n = h_{\frac{1}{n}}$.
My main issue here is that, given the complicated structure of $g_n$, I'm not sure how to evaluate $\int_0^1 f(x)g_n(x) \d{x}$ or bound it properly. I'm also not sure how dense $X_0$ is in $[0,1]$, so I can't seem to guarantee that the measure of the set $Y_\epsilon := \{(x - \epsilon, x + \epsilon) : x \in X_0\}$ tends to zero, which is probably necessary to show my statement.
Any help would be appreciated.
