Behaviour and closed forms of iterated functions

Question

I'm interested in the behaviour of applying the same function repeatedly or oscillating between applying two different functions repeatedly. Let me explain.

If I wanted to know what happens when I square $x$ repeatedly, i.e.: $${{\left({\left({\left(x^2\right)}^2\right)}^2\right)}^2}^{...}$$ I know that this is essentially $$x^{2^{n}},\qquad n=1,2,3,...$$ So I know that if I was to graph $f(x)=x^{2^{4}}$ I'd be graphing what happens if I square $x$ four times.

Similarly, if I wanted to oscillate between squaring and cubing, as in $${{\left({\left({\left(x^2\right)}^3\right)}^2\right)}^3}^{...}$$ then I would find that this is essentially $$x^{\frac{1}{2}\bigl(3-\left(-1\right)^n\bigr)\times6^{\lfloor\frac{n}{2}\rfloor}},\qquad n=1,2,3,...$$ (I had to look up the sequence of numbers, $2,6,12,36,72,...$ that results from $2\times3\times2\times3\,...$ to find a function that would work here). I know that for this if I input $n=3$ I've squared, then cubed, then squared again.

I realise that the examples so far are fairly identical, always producing graphs of $x$ to a positive even number so that as $n\to\infty$ they are the same square bottomed curve in the positive $f(x)$ portion of the plane. However, what I'm more interested in would be repeating a function like $$\sin(\sin(\sin(...\sin(\sin(x))...)))$$ or something which oscillates like $$\sin(\cos(\sin(\cos(...\sin(\cos(x))...))))$$ which can be denoted as $f(x)=\sin(\cos(x))$ and then adopt the iteration notation of $f^{\,n}(x)$ where $f^{\,2}(x)=f(f(x))$ and so on with $n\to\infty$

Can these be written in a simpler form?

I plotted the oscillating version of this repeated function for starting with $\mathrm{sine}$ or starting with $\mathrm{cosine}$ for several iterations and obtained the following results: 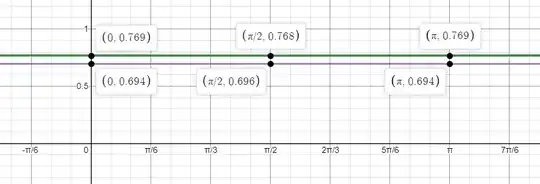As you cans see, after several iterations they are barely sinusoidal in nature at all and are closer to a straight line parallel to the $x$-axis, although there's barely just still some peaks and troughs (some have been highlighted). Is there any reason why they seem to approximate two numbers, namely $y\approx0.695$ for the purple graph and $y\approx0.768$ for the green graph? Is it possible to know these numbers exactly if we could perform the oscillation of functions many many times and solve?

Answer 1

Your question about the 'behaviour' of such iterated functions is too broad to be answered. There are many different functions, with vastly different possible behaviours when iterated.

Iterated functions in general do not appear to have a closed form wrt. the number of iterations, except for isolated cases like $f(x)=x^2\to f^n(x)=x^{(2^n)}$, as you have noted. The compact notation $f^n(x)$ is commonly used to express functions applied to on themselves and can be defined recursively as $f^n(x)=\begin{cases}f(x),&n=1\\f(f^{n-1}(x)),&\text{else}\end{cases}$. This fits with our usual notation of $f^{-1}(x)$ as the inverse of $f$.

The case of $f(x)=\cos x$ leads you to the constant function $f(x)=d$ as $n$ approaches infinity, where $d$ is the fixed point $\cos d=d $, known as Dottie's number (Wikipedia) (Mathworld) (Question 46934). This value is a global attractor, so all $x\in\mathbb{R}$ are mapped towards it when $f$ is iterated. The property holds true for related constants when $\cos$ and $\sin$ are applied one after another. In the case of $f(x)=\sin x$, $f^n(x)$ simply approaches $0$ as $n$ approaches $\infty$.

Whether it is possible to know these numbers "exactly" depends on what you constitute as "knowing", which is again a broad question. Number theory deals in part with how numbers can be "known". For instance, Dottie's number cannot be expressed by the ratio of two integers, nor as a root of an integer-coefficient polynomial. But it can be expressed or defined exactly by:

• Series, e.g. $\frac{\pi}{2}-\frac{1}{4}\pi-\frac{1}{768}\pi^3+\ldots$ and $2\sum_{n=0}^\infty \left( \frac{J_{4n+1}(4n+1)}{4n+1} - \frac{J_{4n+3}(4n+3)}{4n+3}\right)$, with Bessel functions, $J_n$.

• Integrals, e.g. $\frac{\pi}{2}-\int_{0}^{\pi}\left\lfloor\frac{2\left(t-\sin t\right)}{\pi}\right\rfloor\,\mathrm{d}t$, which I found recently.

• Its implicit definition, $d=\cos d$.

Whether this satisfies the criteria for knowing the constant will be subjective. It is very likely that similar properties hold true for the fixed points $x=\sin(\cos x)$ and $x=\cos(\sin x)$.

---

In the case of $\sin^n(x)$, it remains a periodic function, so it can be expressed as an (infinite) Fourier series, e.g., $\sin(\sin x)= 0.880\sin x+0.0391\sin\left(3x\right) + \ldots$. However the coefficients do not have closed forms, as the integral $\int \sin(\sin x)\,\mathrm{d}x$ is nonelementary. Similar series can be made for any combination of $\sin$ and $\cos$ applied successively, which can vastly simplify the functions (depending on what you want to do with them). I have not seen a proof that $\sin^n(x)$ is inexpressible as an elementary function with arguments, $n,x$, but I doubt that it is possible.