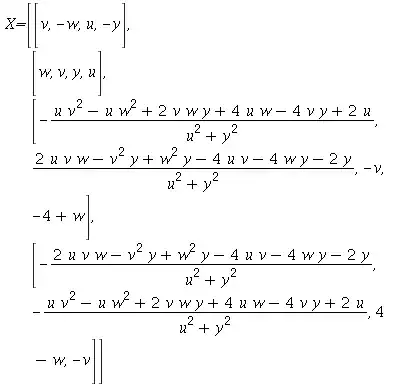3

I am trying to find solutions to an equation of the form:

$$X^2+\theta SX+\lambda I=0$$

Where $X$ is an unknown matrix (what I am trying to solve for), $S$ is a known antisymmetric matrix that squares to $-I$, $I$ is the identity matrix, and $\theta$ and $\lambda$ are real parameters. All the matrices are 4x4.

I can be more specific on $S$:

$$S=\begin{bmatrix} 0 & 0 & 0 & -1 \\ 0 & 0 & 1 & 0 \\ 0 & -1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ \end{bmatrix} $$

Or for a slightly greater level of generality, $S$ is any matrix of the form

$$S=\begin{bmatrix} 0 & -c & -b & -a \\ c & 0 & a & -b \\ b & -a & 0 & c \\ a & b & -c & 0 \\ \end{bmatrix} $$

Where real numbers $a^2+b^2+c^2=1$.

There are a couple similar questions on this site that I could find, but unfortunately I could not understand how to apply the answers there to my problem. Can anyone offer suggestions for how to solve this equation, or even just to discover some properties of the solution even if it cannot be fully determined? (E.g. if the matrix $X$ must turn out to be symmetric or antisymmetric, or a linear combination of $I$ and $S$, or anything like that.) Thanks very much.

Edit: I've been able to show that if $X$ is assumed to be antisymmetric, it must commute with $S$, and that for the specific case where $\lambda=-\theta^2/4$ and $S$ set with parameters $a=1,b=c=0$ this implies the unique solution: $$X=-\frac{1}{2}\theta S$$ The solution given in Rob Israel's answer: $$X=\left( -\frac{1}{2}\theta \pm \sqrt{\frac{\theta^2}{4}+\lambda}\right) S$$ Works as well, but it looks like in addition to that pair, there is an infinite family of antisymmetric solutions when $\lambda > -\theta/4$. Still haven't been able to show whether or not there are any non-skew solutions.

Matt Dickau
  • 2,227

2 Answers2

3

Try $$ X = \frac{-\theta \pm \sqrt{\theta^2+4\lambda}}{2} S $$

Robert Israel
  • 448,999
1

If $S$ is real skew-symmetric and $S^2=-I$, then $S$ is orthogonally similar to the matrix $K=diag(U,U)$ where $U=\begin{pmatrix}0&-1\\1&0\end{pmatrix}$. Then, we may assume that $S=K$.

In general, the equation

$X^2+aSX+bI=0$ ($a,b\in\mathbb{R}$) admits many solutions that are non-skew.

For example, let $a=-4,b=2$. The solutions depend on $4$ real parameters $u,v,w,y$ s.t. $u^2+y^2\not= 0$. More precisely, the general solution has the form

enter image description here

The skew-symmetric solutions are obtained for $v=0,u+X_{3,1}=0$, and then, depend on $2$ parameters.