Imagine I generate $N$ real numbers with a uniform distribution between $0$ and $1$. I sort them in ascending order. And I calculate the differences between each consecutive pair.
For example, for $N = 3$, it would be like this:
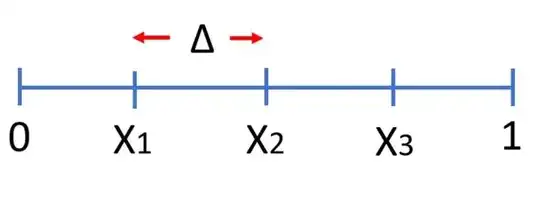
I would like to know what is the expected value of that differences, $\Delta$. Each pair will have a different $\Delta$ but I'm just interested on the average expected value of all $\Delta$.
As I don't know how to calculate it with equations I've done it with a simulation instead (I'm not mathematician nor statistician, I just work with computers). And what I've gotten is: if I have $N$ numbers the average distance between them is $\frac1{1+N}$, and that's also the value between the first number and zero.
I would like to know how to calculate this with equations. Intuitively I think it's the same as calculating $E\left[|X_i-X_j|\right]$ where $X_i$ and $X_j$ are two neighboring numbers in that sample.
In general the expected value is calculated as: $$E[X]=\int_{-\infty}^\infty xf(x)\,dx$$
I think here we should integrate $|X_i-X_j|$ but I don't know $f(x)$, the distribution of the differences, because I can't assume they are independent because we have to sort them and take the nearest pairs. And the absolute value complicates calculations a little bit more.
There is an apparently similar question here but they are speaking about the minimum distance among all pairs.