1

Start with a given "inner" circle of arbitrary radius (blue) centered at C. Surround it by 6 circles of equal radius. This concerns to known issues of circle packing and is a frequently treated interesting topic (s.a. here).

Replace the inner circle with six circles of equal radius, that fit accordingly into the inner circle, i.e.: Change from blue to red constellation.

By which constant factor do the red circles relatively grow/shrink?

Is this a simple task? I'm stuck on finding a general answer.

For clarification I would like to show a geometrical representation I did with GeoGebra:

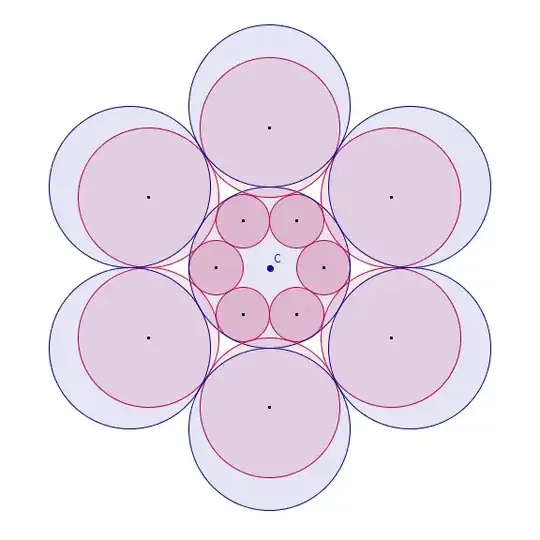
enter image description here

Hope I didn't do something in bad style, please let me know, since this is my first appearance on the stack.

Community
  • 1
JuSchu
  • 13
  • I do not understand the point of the outer blue circles. – Ron Gordon Apr 05 '13 at 18:57
  • I think blue circles is initial state (k=0), and red circles are after one replacement (k=1). He'd like to know the asymptotic behavior as k grows. – alancalvitti Apr 06 '13 at 02:12
  • @alancalvtti: To be honest, I don't expect asymptotic behavior, I expect a constant growing factor so that I get an exponential behavior. The blue circles are of the same (arbitrary) radius as the inner circle labeled with C. This is, as you know, when he have the "typical" hexagonal lattice arrangement in 2D for achieving the highest density. The replacement of the circle C with 6 inner circles (as though there was another smaller inner circle C' that, again, could be replaced by 6 smaller circles) evolves a self-similar pattern with minima and constantly increasing radii, if I'm not wrong. – JuSchu Apr 06 '13 at 12:59
  • @Ron Gordon: The blue circles are for reference to point out why this is not about a question that has already and frequently being answered. – JuSchu Apr 06 '13 at 13:03

1 Answers1

1

Set things up so the inner blue circle is centered at the origin $(0,0)$ with radius $3$, so that the small red circles inside it each have radius $1$, and let one of them be centered at $(2,0)$. The ratio sought is then just the radius $r$ of any of the red circles externally tangent to adjacent inner small red circles. As in your diagram, these red circles extend slightly inside the blue circle of radius $3$ centered at the origin.

Now the coordinates of the center of the first such outer red circle will lie on the ray making an angle of 30 degrees with the positive $x$ axis, and the radius of this first outer red circle is the same as its $y$ coordinate. Therefore the center coordinates may be written as $$P=(r\sqrt{3},r),$$ making use of trig functions of 30 degrees. What we need is an equation satisfied by this point. One can be found by considering the right triangle formed by $P$, the point $(2,0)$, and the projection of $P$ onto the $x$ axis. The formula obtained is then $$(r\sqrt{3}-2)^2+r^2=(r+1)^2.$$ This has two roots, one of which is too small, and the correct root is (using the $+$ in the quadratic equation): $$r = \frac{1+2\sqrt{3}+2\sqrt{1+\sqrt{3}}}{3} \approx 2.5899616.$$ It makes sense this radius (which is also the sought for ratio) should be less than $3$, since drawing pictures makes it clear one has to move the outer circles inward from your sketched larger surrounding blue circles, in order to make them tangent to the smaller circles. I was surprised by the appearance of a "radical inside a radical" in the result.

coffeemath
  • 29,884
  • 2
  • 31
  • 52
  • @coffemath: Thank you very much for your answer! It is clear and concise. It helped me and motivated me to look deeper into the toolboxes of trigonometry and algebra. One question left: Am I right that the "too small root" is just the inverse of the growing factor, thus scaling "inner" circles? – JuSchu Apr 06 '13 at 14:08
  • @coffemath: And,.. I forgot one thing: I'm quite interested why the appearance of a "radical inside a radical" in the result is surprising to you. – JuSchu Apr 06 '13 at 14:12
  • Yes, the "too small root" is that for finding the ratio for the internally tangent series of circles. The poly (the way I set it up) is monic with constant term $3$ which is the radius of the blue circles, so the product of the roots is $3$. As for a radical inside a radical, I guess it's not surprising since $\sqrt{3}$ appears in coefficients from the trig function of 30 degrees, and the poly is quadratic with otherwise integer coeffs. By the way I also did a numerical check using geometer's sketchpad, which allows one to set up dynamic circles and shrink the outer ones in. Got 2.58. – coffeemath Apr 06 '13 at 15:22
  • Is that plain 2.58 = 129/50? Geometer's sketchpad seems to be a beautiful peace of software. I don't know anything about it's internal functions, but how come the difference 2.59 (your solution rounded) vs. 2.58? – JuSchu Apr 06 '13 at 16:42
  • The sketchpad result was indeed $2.59$ (looked again). Note that sketchpad only gives two decimal accuracy in computations, and also I did not get it to plot the exact location of the circle, but had to move it with the mouse until it looked tangent to the two inner circles. My other comment above is not right, namely the equation is $3r^2-(4\sqrt{3}+2)r+3=0,$ which after dividing by $3$ to make it monic gives the product of roots to be $1$, as one should expect if "inner/outer" are interchanged in the ratio. A very interesting question! – coffeemath Apr 06 '13 at 21:37
  • That made me start to read about monic functions, very interisting.The given question arrived when logically questioning the existence of a (static) thing like a circle as given (by itself). So to speak, when questioning the platonic ideal of mathematics (the way I (recurrently) understand Mach).- I know, this is not a chat, I close now. Thanks again for the nice comments and answer. – JuSchu Apr 07 '13 at 17:13
  • I hope it's good practice not to post that elsewhere: I'm wondering, what about the density, when this process is (enumarable) continued? To me it seems, if not wrong, that the density of the packing tends to converge to a maximum of about 0.78346 (simply by continously adding 6 accordingly smaller ones instead of a single one to the inside for comparison), just slightely higher than the densest 7-in-1 packaging with density 0.7777. – JuSchu Apr 08 '13 at 14:57