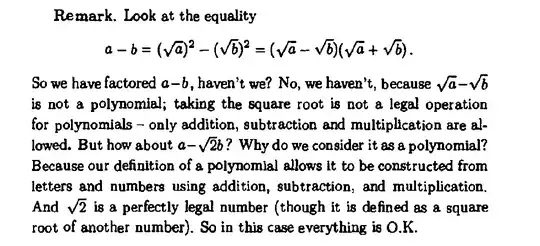0

I'm reading Gelfand's Algebra and it says that the legal operations for polynomials are addition, subtractions and multiplication but taking the square root (i.e. raising the polynomial to the power of $2$) is not a legal operation.

I understood why division (and therefore negative exponents) are not allowed operations in this question but I don't see the 'harm' on allowing raising the polynomials to the power of $ n $

Why is this?

enter image description here

William A. Noble
  • 388
Jon
  • 671
  • What about raising to fractional powers? Do we get a polynomial back in general? – WaveX Jan 23 '20 at 20:05
  • There is no harm, but there is also no need; that operation can be expressed in terms of multiplication. But note that multiplication of polynomials can't be expressed in terms of addition, so you need to take both of those operations as fundamental. Can you see where the difference comes from? – Steven Stadnicki Jan 23 '20 at 20:05
  • 3
    Positive integer powers can be expressed in term of multiplication. The question seems to be about fractional powers (or does the OP really think that $\sqrt{x} = x^2$?) – Robert Israel Jan 23 '20 at 20:07
  • I edited the question adding the relevant piece of text of the book The problem is with doing $ a - b = (\sqrt{a})^2 - (\sqrt{b})^2 $ – Jon Jan 23 '20 at 20:10
  • 1
    You may want to be clearer about what you mean by 'raising to the power of $n$'; there's a wide gap between 'raising to the power of $5$', say, and 'raising to the power of $1/3$'. – Steven Stadnicki Jan 23 '20 at 20:12
  • 2
    @Jon That statement is correct; $a-b=(\sqrt{a}-\sqrt{b})(\sqrt{a}+\sqrt{b})$ is a valid factorization of $a-b$. But it's not a polynomial factorization, because neither factor is a polynomial. – Steven Stadnicki Jan 23 '20 at 20:13
  • As a polynomial, we have $a,b\in\Bbb R$. But in that other form, you must assume $a,b\geq0$. – Andrew Chin Jan 23 '20 at 20:13
  • @AndrewChin Be careful; polynomials can be defined over abstract structures as well. $a-b$ (as a polynomial in $a$ and $b$) is well-defined in many different domains. – Steven Stadnicki Jan 23 '20 at 20:14
  • @StevenStadnicki So the issue here is that the result is not a polynomial because of the fractional exponent (and polynomials only allow positive integers)? Not that raising to the power of a fraction is not allowed? – Jon Jan 23 '20 at 20:21
  • @Jon Raising to the power of a fraction isn't allowed; but raising to the power of an integer is. – Steven Stadnicki Jan 23 '20 at 20:30
  • Taking the square root is not the same as raising the polynomial to the power of $2$, but to the power of $1/2$. Raising a polynomial to a non-negative integer power is allowed, as others have pointed out. – William A. Noble Aug 07 '21 at 06:31

2 Answers2

1

The is no harm. Remember that, if $n\in\mathbb N$ and $P(x)$ is a poynomial, then$$P(x)^n=\overbrace{P(x)\times P(x)\times\cdots\times p(x)}^{\phantom{\text{ times}}n\text{ times}}.$$So, since multiplication is allowed, raising a polynomial to a natural exponent is also allowed.

José Carlos Santos
  • 427,504
  • This makes sense to me so I'm assuming I didn't phrase the question properly. I edited the question adding the relevant piece of text of the book – Jon Jan 23 '20 at 20:12
1

I think you're missing the key notion of abstraction (sometimes aka 'formality') behind polynomials. Suppose that we say 'a polynomial (in one variable) over some base structure is formally an expression of the form $P(x)=\sum_{i=0}^{n_P} p_ix^i$, where $n_P$ is some non-negative integer (so that the notion of summing makes sense) and each $p_i$ is a 'scalar' (i.e., an element of our base structure). Then we can define an addition operation on polynomials $P(x)$ and $Q(x)$ by defining the polynomial $R(x)=\{P+Q\}(x)$ such that $n_R=\max(n_P, n_Q)$ and $r_i=p_i+q_i$ for all $i\leq n_R$ (where any potentially undefined $p_i$ or $q_i$ are taken to be zero). Note that for this definition to make sense, we need to have an addition defined on our base structure, but that's all we need for this formal definition to make sense!*

Similarly, we can formally define the product of two polynomials $P(x)$ and $Q(x)$ by defining the polynomial $R(x)=\{P\cdot Q\}(x)$ such that $n_R=n_P+n_Q$ and $r_i=\sum_{j=0}^i p_jq_{i-j}$ for all $i\leq n_R$ (again taking potentially undefined coefficients as zero). For this definition to make sense, we need to have some sort of multiplication defined on our base structure, but again that's all we need for the formal definition to make sense; as long as we have a 'base structure' with commutative addition and (not necessarily commutative!) multiplication, we can define these formal polynomial-things over that structure, and they also have (commutative) addition and a well-defined multiplication.

Now, there's also an 'evaluation map' that comes with each polynomial; if we call our base structure $B$, then for each polynomial $P(x)$ we can define a function $P^*:B\mapsto B$ by $P^*(b)=\sum_{i=0}^{n_P} p_ib^i$, where we use the multiplication in the base structure to compute the $b^i$ and then the product $p_ib^i$, and the addition in the base structure to compute the sum. This function can be very useful, but it's not the only thing we care about with polynomials; often we really only care about the polynomial as a formal entity!

We can talk about other algebraic structures than polynomials, and of course other functions. But one of the great benefits of polynomials is that all we need on the base structure is addition and multiplication, and they give us a new structure that also has addition and multiplication. For instance, I only defined polynomials in one variable above — but we can think of a polynomial in two variables $x,y$ as a polynomial in $y$ whose coefficients are each polynomials in $x$: $P(x,y)=\sum_{i=0}^{n_P}P_i(x)y^i$.

Often in mathematics, the key to abstraction is to see how small the minimal set of requirements placed on a structure can be in order to do 'interesting' things with it. The idea of a group, for instance, can be motivated by starting with the integers $\mathbb{Z}$ and noticing that the addition operation, all by itself, satisfies some interesting properties (it has an identity and it has inverses), and asking what we can say about structures where all we require is those properties, plus the basic rules we'd like them to obey. Because the requirements are so low, they can be met by things that look nothing like numbers — for instance, the set of symmetries of a dodecahedron.

Polynomials require a little more from the base structure, but the requirements are still small enough that we can apply them to all sorts of interesting structures that aren't just $\mathbb{R}$ (or $\mathbb{C}$).

$$ $$

*For simplicity's sake, we really want commutativity of addition or else we can't necessarily 'force' the ordering of the sum so that it makes sense.

Steven Stadnicki
  • 51,746