1

Let's say that I have the function:

$$f: D \rightarrow \mathbb{R} \hspace{2cm} f(x) = \log_3 x + \log_\sqrt{x} x - \log_\frac{1}{3} x - 6$$

And I have to find the maximum domain of the function, $D$. I see that the function $f$ would simplify to something like this:

$$f(x) = \log_3 x + 2 \log_x x +\log_3 x - 6$$

$$f(x) = 2 \log_3 x + 2 - 6$$

$$f(x) = 2 \log_3 x - 4$$

With this simplified version of the function, I thought it would be no problem to have $x = 1$, since that would mean:

$$f(1) = 2 \log_3 1 - 4 = 2 \cdot 0 -4 = - 4$$

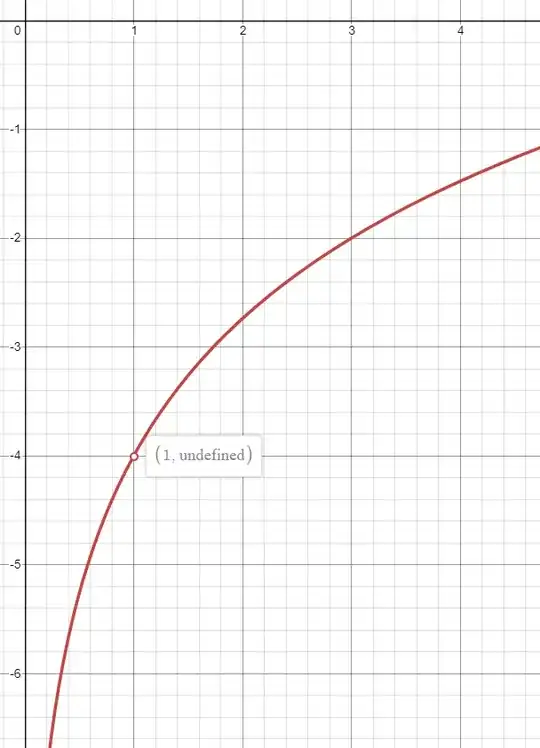
Then I plotted the function (the initial form of the function, not the simplifed one) in Desmos and got this:

enter image description here

To my surprise, the function is undefined in $x_0 = 1$. I know that I plotted the initial function and not the simplified one, but aren't they the same thing? Isn't the simplified version of the function and the function itselft the same? It's not like I added or taken something away.

I know that I can't plug $x = 1$ in the initial form of the function, since we have the condition that the base of the logarithm must be $\ne 1$, but how come I can plug in $x = 1$ in the simplified version and have the function defined in that point? I just don't see how the properties of the function changed because of my simplification, which seemed like such a natural and harmless thing to do.

1 Answers1

4

$\log_a x$ can be expressed simply as $\frac{\ln x}{\ln a}$, so we have $\log_{\sqrt{x}}x=\frac{\ln x}{\ln \sqrt{x}}=2$, for all $x$ in the domain of the function. This excludes nonpositive $x$ or $\sqrt{x}$, which would be undefined in the logarithm, and any $x$ such that $\ln\sqrt{x}=0$ would incur division by zero, which is $x=1$. Thus, $x_0=1$ is not in the domain, $\mathbb{R}^+/\{1\}$. Recall that simplifying a function can appear to change its domain yet the original domain should not change (Question 808384).

Jam
  • 10,325