What is the average radius of the circle containing three random points in a square?

Question

Let $x, y, z$ be three noncollinear points, chosen uniformly and independently from the interior of a unit square. There is a unique circle that passes through $x$, $y$, and $z$. What is the expected value of the radius of this circle?

Answer 1

The expected value of the radius is infinite. In fact, a stronger result can be proved.

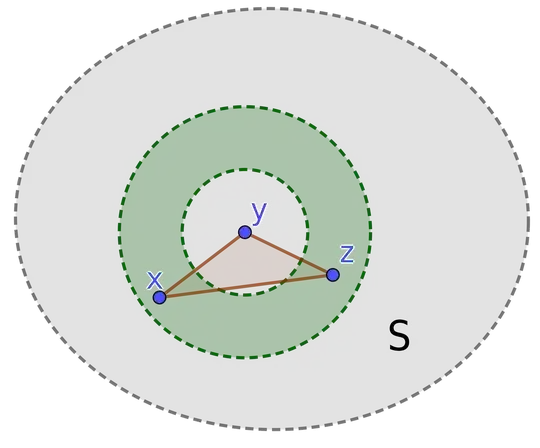
Let $S$ be a nonempty open subset of the plane with finite measure. For any three noncollinear points $x, y, z \in S$, let $R(x, y, z)$ denote the radius of the unique circle containing $x$, $y$, and $z$. Since the probability is zero that three random points are collinear, we can consider $R$ as a random variable on $S^3$. We will show that the expected value of $R$ is infinite.

Choose $\epsilon > 0$ so that $S$ contains a ball of radius $3\epsilon$. Let $V$ be the set of all triples $(x, y, z) \in S^3$ satisfying the following conditions:

• $\operatorname{dist}(y, \partial S) > 2\epsilon$,
• $\epsilon < \operatorname{dist}(x, y) < 2\epsilon$, and
• $\epsilon < \operatorname{dist}(y, z) < 2\epsilon$.

These conditions imply that $x$ and $z$ lie inside an annulus centered at $y$, with inner radius $\epsilon$ and outer radius $2\epsilon$, entirely contained in $S$. See Figure 1.

By continuity of the distance function, $V$ is a nonempty open subset of $S^3$.

By the law of total expectation, $$ \operatorname{E}[R] = \operatorname{E}[R\,|\,V] \operatorname{P}(V) + \operatorname{E}[R\,|\,V^c] \operatorname{P}(V^c) \ge \operatorname{E}[R\,|\,V] \operatorname{P}(V), $$ where $\operatorname{P}(V)$ is the probability that a random element of $S^3$ belongs to $V$. This probability is equal to $\mu(V)/\mu(S^3)$, where $\mu$ is the Lebesgue measure on $\mathbb{R}^6$. Since $\operatorname{P}(V)$ is positive, it suffices to prove that $\operatorname{E}[R\,|\,V]$ is infinite.

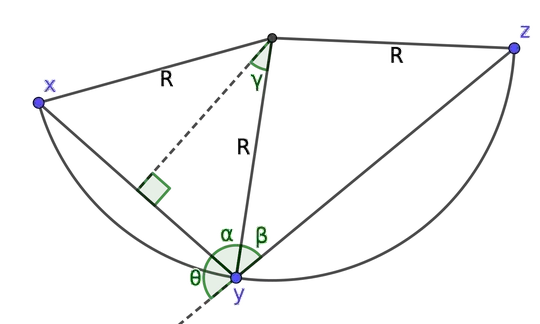
Observe that $V$ has continuous rotational symmetry. The point $z$ can be rotated about the point $y$, keeping both $x$ and $y$ fixed. In symbols, the map $r_{\theta}\colon V\to V$ is an isometry for each $\theta \in [0, 2\pi)$, where $$ r_{\theta}(x, y, z) = (x, y, y + (z - y) e^{i\theta}). $$ This implies that the measure of the angle $xyz$ is uniformly distributed on $[0, \pi]$ when $(x, y, z)$ is drawn from $V$.

Let $(x, y, z) \in V$, and let $\theta = \pi - m(\angle xyz)$, as shown in Figure 2. We may assume without loss of generality that $\operatorname{dist}(x, y) \le \operatorname{dist}(y, z)$. Since $\alpha \ge \beta$, $\theta + \alpha + \beta = \pi$, and $\alpha + \gamma = \pi/2$, it follows that $\gamma \le \theta/2$. Therefore, $$ R = \frac{\operatorname{dist}(x, y)}{2\sin \gamma} > \frac{\epsilon}{2 \sin(\theta/2)} > \frac{\epsilon}{\theta}. $$

But $\theta$ is uniformly distributed on $[0, \pi]$. Therefore, $$ \operatorname{E}[R\,|\,V] \ge \frac{1}{\pi} \int_0^{\pi} \frac{\epsilon}{\theta}\, d\theta = \infty. $$

Since $V$ has positive measure, it follows that $\operatorname{E}[R] = \infty$ as well.

Answer 2

The same analysis as in my answer to Expected area of circle defined by 3 random vertices in unit square? applies. If two of the points are fixed, the radius diverges as the reciprocal of the distance of the third point from the line connecting them, so the integral of the radius over the position of the third point diverges.