Is Inverse (logic) useless?

Question

I always forget the definition of inverse(logic) simply because we don't use it.

Converse is useful because if converse of $p\Rightarrow q$ is true, $p$ and $q$ are equivalent. It's natural to consider converse.

Contraposition is also natural because it is equivalent to $p \Rightarrow q$ and sometimes problem become a little bit easier. (I have never used contraposition, however...)

Then why we consider inverse? Is it important? The concept, inverse is written in every Japanese textbook of high school. So it should be important. But we never use inverse in the proof or discussion.I cannot understand it and always forget it.

Answer 1

Obviously "useful" is a vague concept, but there's a good sense in which the inverse is "logically secondary" - it is not well-defined with respect to logical equivalence. Consider for example the sentences $$A: p\rightarrow \top\quad\mbox{and}\quad B: q\rightarrow\top.$$ $A$ and $B$ are logically equivalent (they're both trivially true), but look at their inverses: $$A^{inv}: \neg p\rightarrow\perp\quad\mbox{and}\quad B^{inv}:\neg q\rightarrow\perp.$$ Remember that "$r\rightarrow\perp$" is logically equivalent to $r$, so we get that $A^{inv}\equiv p$ and $B^{inv}\equiv q$ - so $A^{inv}$ and $B^{inv}$ probably are not logically equivalent, even though $A$ and $B$ are.

What this means is that inversion is really an operation on how the sentence is written as opposed to what it means. By contrast, the contrapositive is well-defined in the sense above: if $p\rightarrow q$ and $r\rightarrow s$ are logically equivalent, then so are $\neg q\rightarrow\neg p$ and $\neg s\rightarrow \neg r$.

---

Of course, all of the above has the implicit assumption that "logical invariance" is a valuable property. I'd say that this is indeed born out in applications, but sociologically speaking this is a relatively modern shift in emphasis as the role of logic moved away from the analysis and classification of arguments - valid or invalid - according to their form and towards pure mathematics. (This isn't to say that this shift in focus is universal, but it is quite substantial.) This is a shift I wholeheartedly endorse, but it's definitely non-trivial.

One great example of that shift in my opinion - indeed, I'd actually consider it one of the most important examples - is the idea of the Lindenbaum algebra, and the convinction that it is an interesting and valuable thing to study. Roughly speaking, the Lindenbaum algebra of a "logical system" $\mathcal{L}$ captures how the various expressions we care about are logically related to one another: elements of the Lindenbaum algebra are "logical equivalence" classes of sentences in $\mathcal{L}$, and the structure comes from those logical operations we can perform, or comparisons we can make, on those equivalence classes (e.g. the Lindenbaum algebra of a theory in classical propositional logic is properly understood as a Boolean algebra). The whole idea behind Lindenbaum algebras is reflective of the shift mentioned above, as syntax takes a back seat to semantics, "semantically-ill-defined" operations aren't even considered, and natural language plays no role whatsoever.

• Incidentally, the exact syntax/semantics dividing line is a bit fuzzy - see e.g. my comments here and here - but I do think it's a valuable one to consider. More to the point, it's a dividing line that itself is indicative of the shift described above.

Answer 2

I definitely would maintain the logical inverse is useful as a concept. But I think the universe of possible "uses" of the logical inverse is far too broad, plus the definition of "useful" in this context far too hazy, to really get into that here.

Here's a schema which might make it easier to remember:

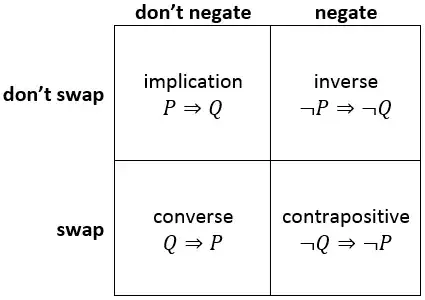
You can consider these four concepts, as the result of 2 distinct "operations", each of which has 2 possibilities (i.e. "applied" or not): $(1)$ negate the antecedent and the consequent, and $(2)$ swap the antecedent and the consequent. Looking at it this way, we can classify these four concepts, in terms of which operation(s) they break down into:

• Implication: $()$
• Inverse: $(1)$
• Converse: $(2)$
• Contrapositive: $(1, 2)$ or $(2, 1)$

Looking at it this way also, I think, makes much clearer another important connection, which is that the contrapositive is the inverse of the converse, or, equivalently, the converse of the inverse.

In your question also brought up the notion of logical transposition, that is, the equivalence between an implication and its contrapositive - or, symbolically, the fact that $(P \Rightarrow Q) \Leftrightarrow (\neg Q \Rightarrow \neg P)$ is a logical theorem. Transposition is the replacement rule that says you can replace any occurrence of $(P \Rightarrow Q)$ in a predicate with $(\neg Q \Rightarrow \neg P)$, without changing its truth value. Our grid fits this rule into a broader context, as one of three possible things that can happen when you start with an implication in the top left square, and take exactly 2 steps in any (non-diagonal) direction.

• Right + Left corresponds to the inverse of the inverse. The inverse of $(P \Rightarrow Q)$ is $(\neg P \Rightarrow \neg Q)$, and the inverse of $(\neg P \Rightarrow \neg Q)$ is $(\neg\neg P \Rightarrow \neg\neg Q)$ which by the double negation rule $\neg\neg P \Leftrightarrow P$ is equivalent to the original implication, $(P \Rightarrow Q)$.
• Down + Up corresponds to the converse of the converse. The converse of $P \Rightarrow Q$ is $Q \Rightarrow P$, and the converse in turn of $Q \Rightarrow P$ brings us back to $P \Rightarrow Q$, which is exactly the original implication.
• Down + Right (in either order) corresponds to the contrapositive. The rule of logical transposition which I just mentioned earlier says that this, too, is equivalent to the original implication.

I'm sure you've noticed what each of these three possibilities has in common: all of them are logically equivalent to the original implication! Any two applications of "inverse" and "converse", in any order, will result in a predicate that's equivalent to the original implication. You can add "contrapositive" to this paradigm easily, too, by converting it into an inverse of a converse.

So, suppose someone asked you: "Given an implication $R = (P \Rightarrow Q)$, what is the inverse of the converse of the converse of the inverse of the contrapositive of the inverse of $R$?" Whoa, that's a doozy! Fortunately, we can use the 2-step rule to quickly and easily figure it out. Tally up the occurrences of each word, and let $I = ``\text{inverses''} + ``\text{contrapositives''}$ and $C = ``\text{converses''} + ``\text{contrapositives''}$.

• If $I$ and $C$ are both even: then you can cancel out all the inverses and converses in pairs of two. The entire predicate is therefore logically equivalent to the original implication, $(P \Rightarrow Q)$.
• If $I$ and $C$ are both odd: then you can cancel out all but one each of the inverses and converses in pairs of two. The remaining single "inverse" and "converse" combine to make the entire predicate equivalent to the contrapositive. And as the contrapositive, the entire predicate is therefore equivalent to the original implication, $(P \Rightarrow Q)$.
• If $I$ is even but $C$ is odd: then you can cancel out all the inverses and all but one of the converses in pairs of two. The remaining single "converse" means the entire predicate is logically equivalent to the converse, $(Q \Rightarrow P)$.
• If $I$ is odd but $C$ is even: then you can cancel out all but one of the inverses and all the converses in pairs of two. The remaining single "inverse" means the entire predicate is logically equivalent to the inverse, $(\neg P \Rightarrow \neg Q)$.

(Final note: I'm sure there are some technical terms for this type of meta-deduction that I'm not aware of and/or not using here. Please feel free to clarify with comments!)