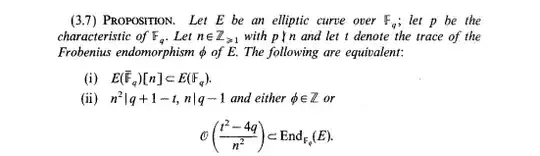1

The text "Nonsingular Plane Cubic Curves over Finite Fields" by Schoof has the following proposition:

enter image description here

The full proof is here:

enter image description here

I can't understand this step of the proof:

enter image description here

I know why the part in blue is true. What is left is the part in red. I'm left to believe that the red 2 equation implies what is inside the red box, but how to prove it?

José
  • 953

1 Answers1

2

Firstly $\frac{\phi-1}{n} \in \operatorname{End}_{\mathbb{F}_q}(E)$ is equivalent to $\mathbb{Z}[\frac{\phi-1}{n}] \subset \operatorname{End}_{\mathbb{F}_q}(E)$ because $\operatorname{End}_{\mathbb{F}_q}(E)$ is a ring.

For a quadratic integer $\alpha$, the norm $N(\alpha) = \alpha\bar{\alpha}$ and trace $T(\alpha) = \alpha+\bar{\alpha}$ appear as coefficients in the minimum polynomial of $\alpha$: $(x-\alpha)(x-\bar{\alpha}) = x^2-T(\alpha)x + N(\alpha)$. The discriminant of this polynomial is $T(\alpha)^2 - 4N(\alpha)$.

The discriminant of the quadratic order $\mathbb{Z}[\frac{\phi-1}{n}]$ is the discriminant of the minimal polynomial of $\frac{\phi-1}{n}$, as calculated in $\color{red}{\mathbf{2}}$ using the above. Note that there is a typo in $\color{blue}{\mathbf{1}}$: the denominator of the norm should be $n^2$, as in the $\color{blue}{\text{blue}}$ box.

In the $\color{red}{\text{red}}$ box, $\mathcal{O}\Big(\frac{t^2-4q}{n^2}\Big)$ denotes the complex quadratic order of discriminant $\frac{t^2-4q}{n^2}$, namely $\mathbb{Z}[\frac{\phi-1}{n}]$.

Ricardo Buring
  • 6,323
  • Thank you. Is the definition of the discriminant of the order as the discriminant of the minimal polinomial equivalent to the definition of the discriminant as the index $[\mathcal{O}_K: \mathcal{O}]$? – José Jan 16 '20 at 01:18
  • 1
    The discriminant of an order with a power basis is (by the usual definition) the determinant squared of a Vandermonde matrix, so it is equal to the discriminant of the minimal polynomial. The relation to the index is $\Delta(\mathcal{O}) = [\mathcal{O}_K : \mathcal{O}]^2 \Delta(\mathcal{O}_K)$. – Ricardo Buring Jan 16 '20 at 12:44
  • I could find the relation $\Delta(\mathcal{O}) = [\mathcal{O}_K : \mathcal{O}]^2 \Delta(\mathcal{O}_K)$ in a book, but there it was the definition of the discriminant. Why is the definition as the discriminant of a minimal polynomial equivalent? – José Jan 19 '20 at 23:13
  • 1
    A usual definition of discriminant can be found e.g. in these lecture notes, Definition 4.4; the relation to the index is explained in the notes, and the computation for a power basis is in Proposition 4.6. – Ricardo Buring Jan 19 '20 at 23:59