Once the Cartesian coordinates of the point in question have been calculated:
$$
(x_p,\,y_p) =
\frac{a\,b}{\sqrt{\left(a\,\sin\theta\right)^2 + \left(b\,\cos\theta\right)^2}}
\,\left(\cos\theta, \, \sin\theta\right)
$$
with $a, \, b > 0, \, 0 \le \theta < 2\pi$ known parameters, essentially two cases can arise.
You are interested in an angle $t \in (-\pi,\,\pi]$:
$$
t = \text{arctan2}\left(x_p/a, \, y_p/b\right)
$$
i.e.
$$
t =
\begin{cases}
\arctan\left(\frac{y_p/b}{x_p/a}\right) - \pi
& \text{if} \; x_p < 0 \, \land \, y_p < 0 \\
\arctan\left(\frac{y_p/b}{x_p/a}\right) + \pi
& \text{if} \; x_p < 0 \, \land \, y_p \ge 0 \\
-\frac{\pi}{2}
& \text{if} \; x_p = 0 \, \land \, y_p < 0 \\
\frac{\pi}{2}
& \text{if} \; x_p = 0 \, \land \, y_p > 0 \\
\arctan\left(\frac{y_p/b}{x_p/a}\right)
& \text{if} \; x_p > 0
\end{cases}
$$
{a, b} = {6, 2};
x[θ_] := a b Cos[θ] / Sqrt[(a Sin[θ])^2 + (b Cos[θ])^2]
y[θ_] := a b Sin[θ] / Sqrt[(a Sin[θ])^2 + (b Cos[θ])^2]
Plot[ArcTan[x[θ] / a, y[θ] / b], {θ, 0, 2π}, AxesLabel -> {"θ", "t(θ)"}]
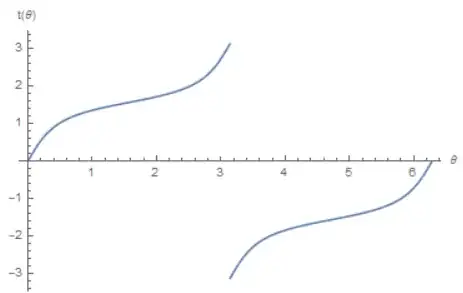
therefore, known the integration extremes $t_1 \le t_2$, the length of the ellipse arc is equal to:
if the arc does not cut the negative semi-axis of x:
$$
\mathcal{L} = \int_{t_1}^{t_2}
\sqrt{\left(a\,\sin t\right)^2+\left(b\,\cos t\right)^2}\,\text{d}t \,;
$$
if the arc cuts the negative half-axis of x:
$$
\mathcal{L} = \int_{-\pi}^{t_1}
\sqrt{\left(a\,\sin t\right)^2+\left(b\,\cos t\right)^2}\,\text{d}t +
\int_{t_2}^{\pi}
\sqrt{\left(a\,\sin t\right)^2+\left(b\,\cos t\right)^2}\,\text{d}t \,.
$$
You are interested in an angle $t \in [0,\,2\pi)$:
$$
t =
\begin{cases}
\text{arctan2}\left(x_p/a, \, y_p/b\right) + 2\pi
& \text{if} \; \text{arctan2}\left(x_p/a, \, y_p/b\right) < 0 \\
\text{arctan2}\left(x_p/a, \, y_p/b\right)
& \text{if} \; \text{arctan2}\left(x_p/a, \, y_p/b\right) \ge 0 \\
\end{cases}
$$
i.e.
$$
t =
\begin{cases}
\arctan\left(\frac{y_p/b}{x_p/a}\right) + \pi
& \text{if} \; x_p < 0 \\
\frac{3\pi}{2}
& \text{if} \; x_p = 0 \, \land \, y_p < 0 \\
\frac{\pi}{2}
& \text{if} \; x_p = 0 \, \land \, y_p > 0 \\
\arctan\left(\frac{y_p/b}{x_p/a}\right) + 2\pi
& \text{if} \; x_p > 0 \, \land \, y_p < 0 \\
\arctan\left(\frac{y_p/b}{x_p/a}\right)
& \text{if} \; x_p > 0 \, \land \, y_p \ge 0
\end{cases}
$$
{a, b} = {6, 2};
x[θ_] := a b Cos[θ] / Sqrt[(a Sin[θ])^2 + (b Cos[θ])^2]
y[θ_] := a b Sin[θ] / Sqrt[(a Sin[θ])^2 + (b Cos[θ])^2]
t[x_, y_] := Piecewise[{{ArcTan[x, y] + 2π, ArcTan[x, y] < 0},
{ArcTan[x, y], True}}]
Plot[t[x[θ] / a, y[θ] / b], {θ, 0, 2π}, AxesLabel -> {"θ", "t(θ)"}]
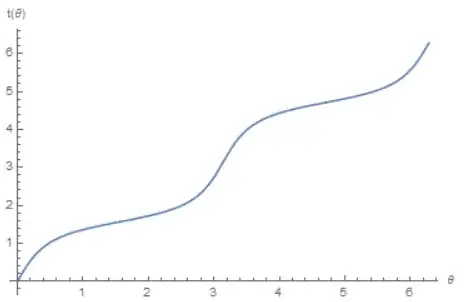
therefore, known the integration extremes $t_1 \le t_2$, the length of the ellipse arc is equal to:
if the arc does not cut the positive semi-axis of x:
$$
\mathcal{L} = \int_{t_1}^{t_2}
\sqrt{\left(a\,\sin t\right)^2+\left(b\,\cos t\right)^2}\,\text{d}t \,;
$$
if the arc cuts the positive half-axis of x:
$$
\mathcal{L} = \int_{0}^{t_1}
\sqrt{\left(a\,\sin t\right)^2+\left(b\,\cos t\right)^2}\,\text{d}t +
\int_{t_2}^{2\pi}
\sqrt{\left(a\,\sin t\right)^2+\left(b\,\cos t\right)^2}\,\text{d}t \,.
$$

