4

Choose two real numbers $a$ and $b$ satisfying $1<a<3$ and $-1<b<1$ randomly.

Find the probability that the polynomial $x^2+ax+b$ has two real roots.

NB: uniform distribution

bp99
  • 1,107
Diakolo Belya
  • 59
  • 4
  • 3
    What have you got so far? When does $x^2 + ax + b = 0$ have two real solutions? – bp99 Jan 07 '20 at 10:57
  • 2
    So, if you know the distributions of $a$ and $b$, what would you say is the probability $$ P(a^2 - 4b > 0) $$ ? I would consider starting by making an auxiliary variable $z=a^2 - 4b$ and then consider its CDF. – Matti P. Jan 07 '20 at 11:10
  • I am French-speaking and it may be that my English is not well understood. Otherwise talking about uniform distribution is well in the domain of probability in my opinion.(?) – Diakolo Belya Jan 07 '20 at 11:16

2 Answers2

4

Assuming that the distribution is uniform, you just need to compute the ratio between the shadowed area in the picture and the area of the rectangle.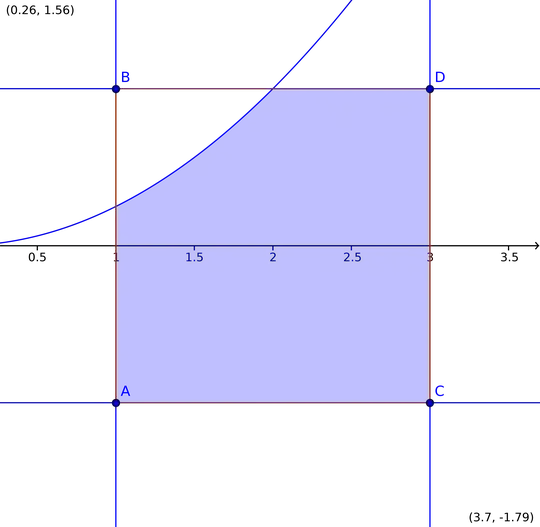enter image description here

Looking at $a,b$ as random variables, you just have that \begin{align*} P(a^2-4c>0)=& \frac{1}{6} \left(3+ \int_1^3 \frac 14 a^2 da \right)=\frac{43}{48} \end{align*}

PierreCarre
  • 20,974
  • 1
  • 18
  • 34
  • Why does this method work? I'd be happy to expand my knowledge! – uriyabsc Jan 07 '20 at 11:21
  • @uiyaba The $(a,b)$ points falling in the shadowed area are the ones that work. In continuous distributions, the count is substituted by the integral (area). The ration I propose is just the "number" of favorable situations divided by the total "number" of possibilities. – PierreCarre Jan 07 '20 at 11:24
  • This curve conforms well to my simulation results by the Monte Carlo method. Thank you very much Sir. – Diakolo Belya Jan 07 '20 at 11:32
  • @uriyaba, you want $P(a^2>4b) = \iint_{x^2>4y}f_{a,b}(x,y),dxdy$, and assuming $a$ and $b$ are independent, this is equal to $\iint_{x^2>4y}f_{a}(x)f_b(y),dxdy$ and since $a$ and $b$ are uniform, this is just a ratio of area of $x^2>4y$ inside a square and the area of the whole square. – Ennar Jan 07 '20 at 11:37
  • 2
    @Diakolo Belya, you mean, your Monte Carlo simulation conforms well to the curve. – Ennar Jan 07 '20 at 11:43
  • Yes Sir . How can i post an image, can you please explain the procedure! Just to show the codes and the result of the Monte Carlo simulation. – Diakolo Belya Jan 07 '20 at 12:00
  • 1
    @Diakolo Belya, I would start by looking at the help center. Follow the link there and go to the bottom. – Ennar Jan 07 '20 at 12:04
1

Let $\left[x^{2}>4y\right]$ denote the function with arguments $x,y$ that takes value $1$ if $x^{2}>4y$ and takes value $0$ otherwise.

Then:

$$\begin{aligned}P\left(a^{2}>4b\right) & =\mathbb{E}\left[a^{2}>4b\right]\\ & =\frac{1}{4}\int_{1}^{3}\int_{-1}^{1}\left[x^{2}>4y\right]dydx\\ & =\frac{1}{4}\int_{1}^{3}\int_{-1}^{\min\left(\frac{1}{4}x^{2},1\right)}dydx\\ & =\frac{1}{4}\int_{1}^{3}\min\left(\frac{1}{4}x^{2},1\right)+1dx\\ & =\frac{1}{4}\int_{1}^{2}\left(\frac{1}{4}x^{2}+1\right)dx+\frac{1}{4}\int_{2}^{3}2dx\\ & =\frac{1}{4}\left[\frac{1}{12}x^{3}+x\right]_{1}^{2}+\frac{1}{2}\\ & =\frac{19}{48}+\frac{24}{48}=\frac{43}{48} \end{aligned} $$

drhab
  • 151,093
  • Thank sir , this is well the result i got by simulation by Monte Carlo method's. – Diakolo Belya Jan 07 '20 at 11:31
  • What do you think Sir, about the method which consists by passing through the surface generated by the discriminant in 3d-space and taking the ratio of the area corresponding to the positive values of the discriminant over the total area? Is it more consistent than the method using a flat surface? – Diakolo Belya Jan 07 '20 at 11:56
  • 1
    I think that no method exists that can be labeled as "more consistent than the method used in this answer". – drhab Jan 07 '20 at 12:00
  • Ok thinks very much. I forgot the say that by that method, i got a result near 0.9 and here 43/48~=0.89583. – Diakolo Belya Jan 07 '20 at 12:05