As discussed in the other thread you linked to, the reverse of an $n$-digit prime can asymptotically be regarded as a random $n$-digit number in which the first digit is uniformly randomly drawn from $1$, $3$, $7$, $9$ and the remaining digits are uniformly randomly drawn from all digits $0$ through $9$.
Consider one “decade” $\left[10^{n-1},10^n\right]$ of $n$-digit numbers at a time. As a first approximation, we can consider the density of primes on this interval to be constant. This should yield the asymptotic result, since the density $\frac1{\log x}$ varies arbitrarily slowly for $x\to\infty$. Then the primes are equidistributed over the interval, and since the four blocks of reversed primes in $\left[d\cdot10^{n-1},(d+1)\cdot10^{n-1}\right]$ for $d=1,3,7,9$ are symmetric about the centre $\frac{11}2\cdot10^{n-1}$ of the interval, we expect half the primes to be less than their reverse. That explains your values close to $\frac12$ at powers of $10$, where you've counted only entire decades.
To explain the slight deviation from $\frac12$, let’s improve the approximation and include a linear term in the expansion of $\frac1{\log x}$:
$$
\frac1{\log\left(a\cdot10^{n-1}\right)}\approx\frac1{\log\left(\frac{11}2\cdot10^{n-1}\right)}-\frac1{\frac{11}2}\cdot\frac1{\log\left(\frac{11}2\cdot10^{n-1}\right)^2}\;.
$$
The linear term yields a contribution
$$
-\frac2{11}\cdot\frac1{\log\left(\frac{11}2\cdot10^{n-1}\right)}\cdot\frac14\cdot\frac19\\\left(\int_1^1\left(x-\frac{11}2\right)\mathrm dx+\int_1^2(2-x)\left(x-\frac{11}2\right)\mathrm dx\\+\int_1^3\left(x-\frac{11}2\right)\mathrm dx+\int_3^4(4-x)\left(x-\frac{11}2\right)\mathrm dx\\+\int_1^7\left(x-\frac{11}2\right)\mathrm dx+\int_7^8(8-x)\left(x-\frac{11}2\right)\mathrm dx\\+\int_1^9\left(x-\frac{11}2\right)\mathrm dx+\int_9^{10}(10-x)\left(x-\frac{11}2\right)\mathrm dx\right)\\
=\frac{61}{594}\cdot\frac1{\log\left(\frac{11}2\cdot10^{n-1}\right)}\;,
$$
where each line corresponds to one of the four blocks of primes. Since you went up to $n=10$, we'd expect this to have decreased to
$$
\frac{61}{594}\cdot\frac1{\log\left(\frac{11}2\cdot10^9\right)}\approx0.0046\;,
$$
for a total fraction $0.5046$ of primes less than their reverse, in rough agreement with your result $0.506$ (which contains higher contributions from the shorter lower decades, and also the higher-order terms neglected above).
This fraction is minimal, since whenever we count parts of a decade the primes are lower in the decade whereas their reverses are still equidistributed over the same four blocks, so in this case the primes are more likely to be less than their reverse. To find the point at which this effect is maximal, revert to the approximation of constant prime density and consider a decade partially counted up to $a\cdot10^{n-1}$.
Since we take the prime density as constant, we can omit it from the counts, as it would cancel in the ratio. That's as if we were counting all numbers instead of just the primes (but with the reverses still starting only with $1,3,7,9$). From the lower decades we have a total of $10^{n-1}$ numbers, of which $\frac12\cdot10^{n-1}$ are less than their reverses. From the partially counted decade, we have a total of $(a-1)10^{n-1}$ numbers. If $1\le a\le2$, then
$$
10^{n-1}\cdot\frac14\int_1^a(3+(2-x))\mathrm dx=\frac{10^{n-1}}8(a-1)(9-a)
$$
of them are less than their reverse, for a total fraction of
$$
\frac{\frac12+\frac18(a-1)(9-a)}{1+(a-1)}=\frac{-a^2+10a-5}{8a}\;.
$$
We can do this analysis for each of the intervals within and between the blocks of reversed primes. For $2\le a\le3$ we get an additional count of $10^{n-1}\cdot\frac34(a-2)$, for a fraction
$$
\frac{\frac12+\frac18(2-1)(9-2)+\frac34(a-2)}{1+(a-1)}=\frac{6a-1}{8a}\;.
$$
For $3\le a\le4$ we get an additional count of
$$
10^{n-1}\cdot\frac14\int_3^a(2+(4-x))\mathrm dx=\frac{10^{n-1}}8(a-3)(9-a)\;,
$$
for a fraction
$$
\frac{6\cdot3-1+(a-3)(9-a)}{8a}=\frac{-a^2+12a-10}{8a}\;.
$$
For $4\le a\le7$ we get an additional count of $10^{n-1}\cdot\frac12(a-4)$, for a fraction
$$
\frac{-4^2+12\cdot4-10+4(a-4)}{8a}=\frac{4a+6}{8a}\;.
$$
For $7\le a\le8$ we get an additional count of
$$
10^{n-1}\cdot\frac14\int_7^a(1+(8-x))\mathrm dx=\frac{10^{n-1}}8(a-7)(11-a)\;,
$$
for a fraction
$$
\frac{4\cdot7+6+(a-7)(11-a)}{8a}=\frac{-a^2+18a-43}{8a}\;.
$$
For $8\le a\le9$ we get an additional count of $10^{n-1}\cdot\frac14(a-8)$, for a fraction
$$
\frac{-8^2+18\cdot8-43+2(a-8)}{8a}=\frac{2a+21}{8a}\;.
$$
For $9\le a\lt10$ we get an additional count of
$$
10^{n-1}\cdot\frac14\int_9^a(0+(10-x))\mathrm dx=\frac{10^{n-1}}8(a-9)(11-a)\;,
$$
for a fraction
$$
\frac{2\cdot9+21+(a-9)(11-a)}{8a}=\frac{-a^2+20a-60}{8a}\;.
$$
To summarize, the fraction of primes less than their reverse up to $a\cdot10^{-n}$ is asymptotically
$$
\frac1{8a}\cdot
\begin{cases}
-a^2+10a-5 & 1\le a\le2\;,\\
6a-1 & 2\le a\le3\;,\\
-a^2+12a-10 & 3\le a\le4\;,\\
4a+6 & 4\le a\le7\;,\\
-a^2+18a-43 & 7\le a\le8\;,\\
2a+21 & 8\le a\le9\;,\\
-a^2+20a-60 & 9\le a\lt10\;.\\
\end{cases}
$$
The maximum occurs in the interval $3\le a\le4$. Setting the derivative of
$$
\frac{-a^2+12a-10}{8a}=\frac18\left(-a+12-\frac{10}a\right)
$$
to zero yields $a=\sqrt{10}$, as you suspected. The maximum proportion of primes less than their reverse is
$$
\frac18\left(-\sqrt{10}+12-\frac{10}{\sqrt{10}}\right)=\frac{6-\sqrt{10}}4\approx0.709\;,
$$
again in rough agreement with your results.
I find it remarkable that this maximum occurs at the geometric mean of the decade. If we consider the proportion of all numbers, not just primes, that are less than their reverse, so that the reverses are equidistributed over the decade and not concentrated in four blocks, this proportion comes out as
$$
\frac{\frac12+\int_1^a\frac{10-x}9\mathrm dx}{8a}=\frac{-a^2+20a-10}{18a}\;.
$$
Remarkably, since the first and last term in the numerator are the same as for the primes and the middle term is constant, the maximum is in the same place, at $a=\sqrt{10}$. The maximal proportion in this case is
$$
\frac1{18}\left(-\sqrt{10}+20-\frac{10}{\sqrt{10}}\right)=\frac{10\sqrt{10}}9\approx0.760\;,
$$
considerably higher than for the primes.
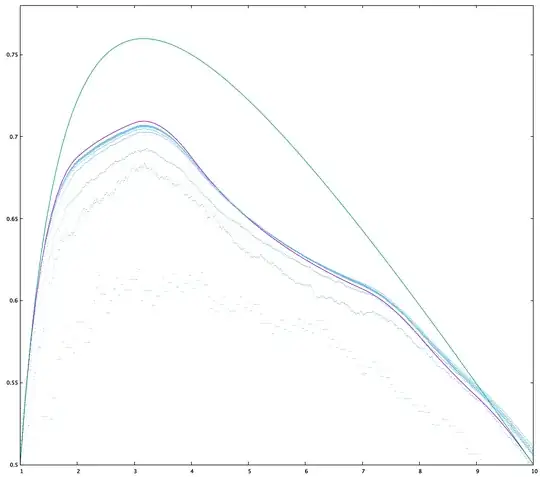
Here's a plot of the proportion of the primes that are less than their reverse for the decades up to $10^{11}$. The blue dots are the actual data for the primes, the purple curve shows the above asymptotic result for the primes, and the green curve shows the above asymptotic result for all numbers for comparison, with the maximum in the same place. The convergence to the asymptotic curve for the primes is clearly discernible. The proportion up to $10^{11}$ is about $0.5052$, consistent with your data and in rough agreement with the linear approximation above.