Here is a solution that has a strong similarity with the solution by @Aryaman Maithani but uses a straightforward method associated with a so-called "Markov chain" :
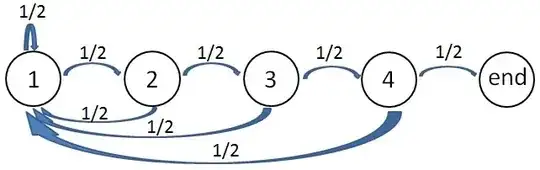
with 4 states with remaining hope (states (1),(2),(3),(4)), and last state where we fall if we have had four consecutive ones.
Let us start with state (1) where we are either waiting for the first figure or are in a situation where the last discovered digit is a zero :
Being in state (2), which means that we have a single 1,
either the new figure is a zero (probability 1/2) and we jump back to state (1)
or it is a one and jump to state (3), etc.
How do we express the different moves in the automata ? By a matrix rendering the probability combinations (total probability law) applied to the initial state with a vector $(1,0,0,0,0)$ which means that, with probability 1, we are in state (1) right at the beginning of the "game". Taking $a:=1/2$, we have at the end of the $k$-th iteration, the following probabilities $p_1, p_2, p_3,p_4,p_{end}$ of being in states (1), (2), (3), (4) or "end" resp.:
$$\begin{pmatrix}p_1\\p_2\\p_3\\p_4\\p_{end}\end{pmatrix}=\left(\begin{array}{cccc|c} a& a&a&a&0\\a&0&0&0&0\\0&a&0&0&0\\0&0&a&0&0\\ \hline 0&0&0&a&1\end{array}\right)^k\begin{pmatrix} 1\\0\\0\\0\\0\end{pmatrix}\tag{1}$$
Can you "end it" (pun intended) from here knowing that a natural denominator you will find is $2^{17}$ (number of numbers with 17 decimal digits) and that you have to iterate $k$ times to finally find a fraction expressing the probability of unfavorable cases : therefore the numerator of this fraction counts the number of unfavorable cases...
Remarks :
The sum of every line of matrix (1) is equal to 1. One finds often the other convention (use transposition).
Formula (1) is completely analogous to the formula proposed in the other answer (the analogy is striking when you consider the upper left block).
