1

I was browsing XKCD and came across this comic discussing differentiation and integration:

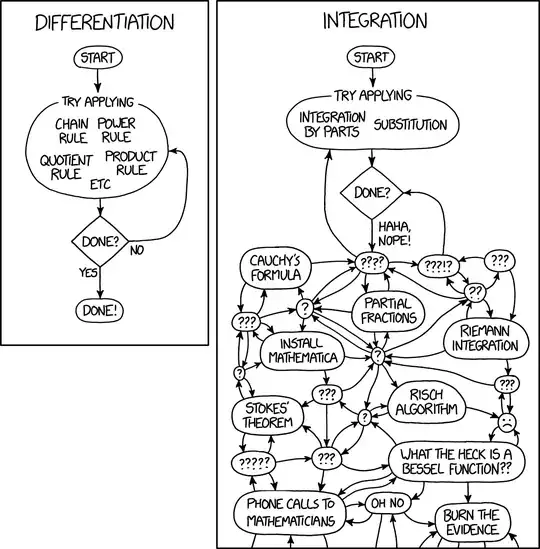
XKCD comic

This resonates true with my college-level understanding of calculus: differentiation is very procedural, while integration sometimes requires a stroke of insight. It appears to me that given a mathematical expression, it's possible to transform it into a computer-science style expression tree and recursively compute the derivative. However, that doesn't seem sensible to do for integration.

Is it an artifact of how we teach calculus? Is it an artifact of how calculus was created/discovered? I could believe that differentiation looks easier because most calculus classes only work with elementary functions and there are simple rules for elementary functions. Or perhaps there is a "master theorem" for integration that is too complicated to cover in engineering calculus (which is my background).

On the other hand, is there a proof (or intuition) as to why integration is more difficult and/or impossible in some cases? If integration is mostly defined or encountered as the reverse of differentiation, then I could believe integration is more difficult in the same way most believe P != NP (with a stretch of metaphor).

Mark Miller
  • 215

1 Answers1

1

I don't know if the question has any definitive answer, but here's one take: If you're calculating a derivative, you're assuming very much of the function. It must be differentiable, and therefore continuous. If you're integrating, you assume much less. Every differentiable function is integrable, every continuous function too, and many many more.

Extreme example would be a continuous function to which we don't know any closed form integral.

user3010768
  • 164
  • Even extremely well-behaved functions, given in terms of elementary functions, may fail to have an antiderivative expressed in elementary terms. – Fimpellizzeri Jan 03 '20 at 17:28
  • F., Yes that's true. The original question isn't answered by this, but this at least says that integrating should be a priori harder, since there are very exotic funtions that are integrable. – user3010768 Jan 03 '20 at 17:33