A circle's area could be defined as $\pi$ times $r$ times $r.$ However, how do we get this valuation? This video shows one way we can find the area of a circle. I highly encourage you to watch it as it will be vital to understand it before continuing.
In the video, they talk about how we can create a circle within the circle, and even smaller circles within that circle. Basically like an onion, with multiple rings. You would then take all the rings, and place them in such a way that it would form a triangle. The height would be the circumference, or $\pi$ times two times $r$, and the length would be $r.$
So using the two values, we can find the area of the triangle, and therefor find the area of the circle.
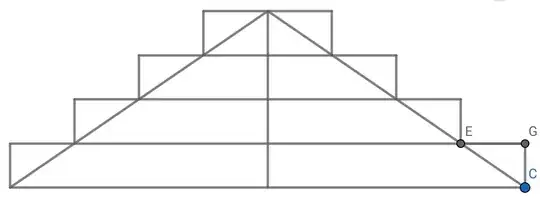
However, I have a question on this. When you draw out the rectangles, no matter how many there are, they should look something like this:
__
__ | |
| || |
Notice the height difference? Of course, the more rectangles we create, the smaller the gap, but the gap will always be there. Does that mean, for this proof at least, that the area of the triangle is a little smaller than $\pi$ times $r$ times $r$?
And if it is, could we express it as a limit? Perhaps as the limit of the number of rectangles reaches infinity, the area becomes closer and closer to a circle's?