Plane intersecting a $95^\circ$ cone at right angles:
I'm trying to build a homemade tracking platform for my telescope. I'm hoping that I can come up with an equation that I can use to cut a bearing for it on a milling machine. I think it is a hyperbola generated by the intersection of a plane to a cone. The plane intersects the cone $34.25$ inches from the tip and at a right angle. The cone has an angle of $95^\circ$ (twice my latitude).
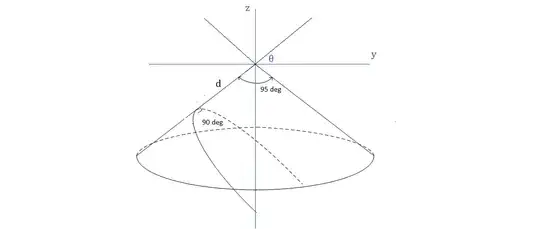
Here's a side view of the scenario. Point $O$ is the tip of your cone. The cone's axis is the vertical through $O$; the horizontal represents the plane perpendicular to the axis at $O$. Angle $\theta$ is half the cone angle; so, it's your latitude. The cutting plane is represented by $\overleftrightarrow{VV'}$, which cuts the cone at a point at distance $d$ from $O$.
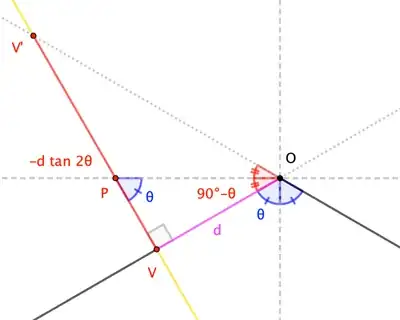
This answer explains that the eccentricity of a conic —call it $e$— is given by the angles made by the cone and by cutting plane with that horizontal plane. Here, we have $$e = \frac{\sin\angle VPO}{\sin\angle POV} = \frac{\sin\theta}{\sin(90^\circ-\theta)}=\frac{\sin\theta}{\cos\theta}=\tan\theta \tag{1}$$
The hyperbola's transverse axis is given by $$|VV'| = d\tan\angle VOV' = d\tan(180^\circ-2\theta)=-d\tan 2\theta \tag{2}$$
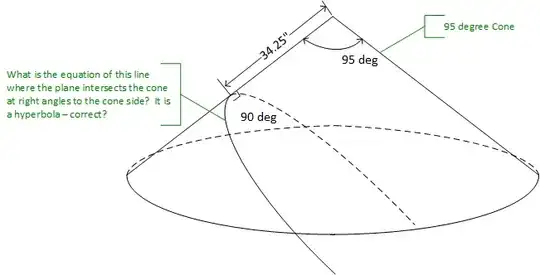
(Note that $2\theta$ here is $95^\circ$, an obtuse angle with a negative tangent; thus, the negative sign in $(2)$ makes the value positive, as expected.)
Choosing convenient coordinates in the cutting plane ($x$-axis aligned with $\overline{VV'}$, origin at the segment's midpoint), the equation of the hyperbola in that plane is
$$\frac{x^2}{a^2}-\frac{y^2}{b^2} = 1 \tag{3}$$ where $$\begin{align} a &= \frac12|VV'| &&= -\frac12d\tan 2\theta \\[4pt] b &= a\sqrt{e^2-1} &&= -\frac12d\tan2\theta\sqrt{\tan^2\theta-1}=\frac{d}{\sqrt{1-\cot^2\theta}} \end{align} \tag{4}$$
In the particular case where $\theta = 95^\circ/2 = 47.5^\circ$ and $d = 34.25$, this gives $$a = 195.74 \qquad b = 85.5349$$ Since $e = 1.09131$, this is "close" to a parabola near the vertex, although the resemblance fails quickly, as the hyperbola approaches asymptotes and a parabola, of course, doesn't.
An equation of a right cone with apex at the origin, axis along the $z$-axis and aperture angle $2\phi$ is $x^2+y^2=z^2\tan^2\phi$, which can be represented by the matrix $Q=\operatorname{diag}(1,1,-\tan^2\phi,0)$. Setting $\mathbf x = (x,y,z,1)^T$, the equation can then be written in the matrix form $\mathbf x^TQ\mathbf x=0$.
We can similarly write the parameterization $\mathbf p_0+s\mathbf u+t\mathbf v$ of a plane as $$\mathbf X = \begin{bmatrix}\mathbf u&\mathbf v&\mathbf p_0\\0&0&1\end{bmatrix} \begin{bmatrix}s\\t\\1\end{bmatrix} = M\mathbf x.$$ This amounts to defining a coordinate system on the plane with $\mathbf p_0$ as the origin. In this coordinate system, the conic defined by the intersection of the cone and plane has the equation $$(M\mathbf x)^TQ(M\mathbf x) = \mathbf x^T(M^TQM)\mathbf x= 0,$$ i.e., this conic has the matrix $M^TQM$.
A simple and convenient choice for $M$ for this problem is $$M=\begin{bmatrix}0 & -\cos\phi & -d\sin\alpha \\ 1 & 0 & 0 \\ 0 & \sin\phi & -d\cos\alpha \\ 0&0&1 \end{bmatrix}.$$ This makes the $y$-axis on the plane the transverse axis of the hyperbola and places the origin at the vertex of the lower branch, which is a distance $d$ down the side of the cone. We then have $$M^TQM = \begin{bmatrix}1&0&0 \\ 0&\cos2\phi \sec^2\phi & d\tan\phi \\ 0&d\tan\alpha&0\end{bmatrix}.$$ This corresponds to the equation $$x^2+y^2\cos2\phi\sec^2\phi+2dx\tan\phi=0.$$ Using any of the usual methods we can find that the center of this conic is at $\left(0,-\frac d2\tan2\phi\right)$. Translating the origin to this point produces the equation $$x'^2 + y'^2\cos2\phi\sec^2\phi=d^2\sec2\phi\sin^2\phi.$$ For $\phi\gt\pi/4$, this is a hyperbola (although since $\phi$ is close to $\pi/4$ it is very close to a parabola). From this equation, we can find that the transverse half-axis length is $-\frac d2\tan2\phi$ and conjugate half-axis length is ${d\over\sqrt{1-\cot^2\phi}}$. In your case, $\phi=95°/2=47.5°$ and $d=34.25$, so the half-axis lengths work out to be approximately $195.74$ and $85.54$, respectively.
In Cartesian coordinate, the surface equation of the cone is
$$z^2 = \tan^2\theta(x^2+y^2)\tag 1$$
where $\theta = \frac {85}2=42.5$ deg. The normal vector to the surface of the cut is $n =(0, \cos\theta, \sin\theta)$ and the vertex point of the cut is $V(0, -d\cos\theta, -d\sin\theta)$. Then, for any point $P(x,y,z)$ in the plane of the cut, $n\cdot(P-V)=0$ holds. Explicitly, the equation of the plane is
$$y\cos\theta+z\sin\theta+d=0\tag 2$$
Thus, the equation for the edge of the cut is given by the intersection of the cone (1) and the plane (2), which is a hyperbola. For instance, it is seen from its projection onto the $xy$-plane obtained by eliminating $z$,
$$x^2 - (\cot^4\theta - 1)y^2 +2d\csc\theta\cot^3\theta\> y - d^2\csc^2\theta \cot^2\theta= 0$$
which is a hyperbola because $\cot^4\theta - 1>0$.
