3

What are the conditions on $a_1, b_1, a_2, b_2, a_3, b_3$ and on the initial values $x_1, x_2$ for $x_n$ to converge to a value different from zero? We can assume that $a_1=1$. Also we need $a_1 = a_2 - a_3$ and $b_1 = b_2 - b_3$, but this is not enough to guarantee convergence.

We can even assume that $x_1=0, x_2 = 1$, see detailed discussion on these recurrences in my previous question, here. In short, there is only 3 free parameters, characterizing all the recurrences that do converge.

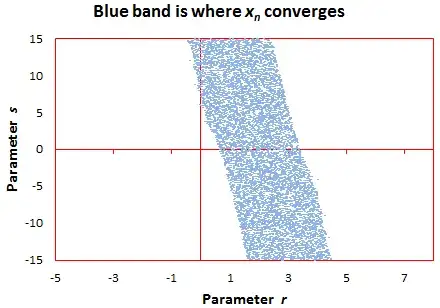
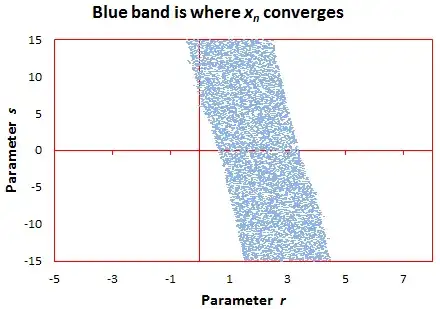
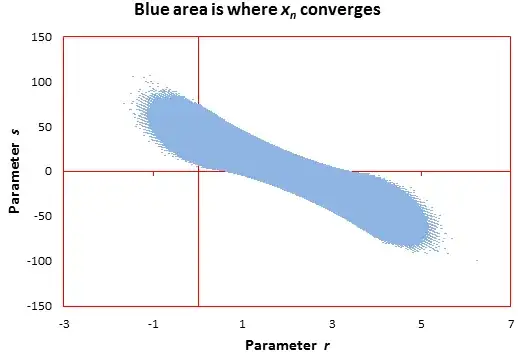
As a starting point, see the chart below for

$$2(n+2)x_{n+2}=(r (n+2) + s)x_{n+1} + ((2-r)(n+2)-s)x_n$$

with $x_0=0, x_1=1$. This 2-dimensional plot represents one slice of all the possible 3-dimensional parameter representations leading to divergence. The X-axis represents $r$, the Y-axis represents $s$. I tried with 400,000 values of $(r, s)$ to check which ones result in actual convergence. The blue dots represent the points $(r,s)$ such that $|x_{40} - x_{39}|<0.000001$. The blue area is full of holes because I only used 400,000 values of $(r, s)$ in this experiment. If you use 10,000,000 values, the boundaries will be smoother, and the holes in the blue area will vanish.

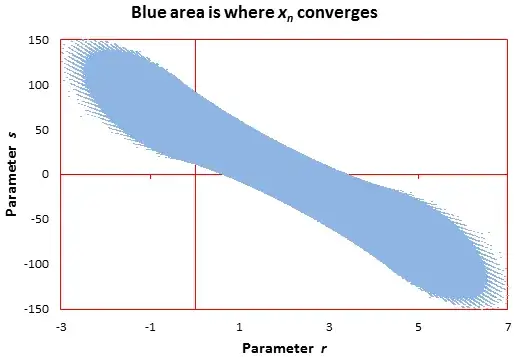
enter image description here

These recurrences can be represented by generalized hypergeometric functions, and according to Wikipedia, the convergence status is typically studied separately for each recurrence. Yet my chart suggests that there is a general law governing the convergence (or lack of) for these recurrences. It is an interesting math problem, and also of interest to statisticians who are interested in estimating the boundaries (in the parameter space) of the convergence region, and test whether the boundaries are parallel lines.

More cases

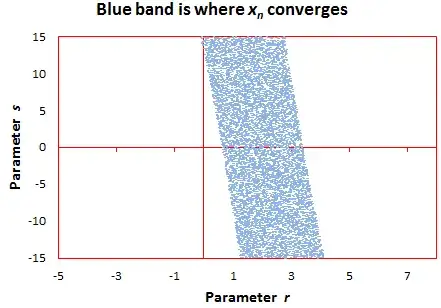
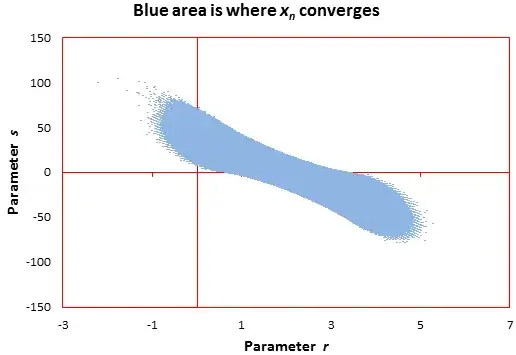
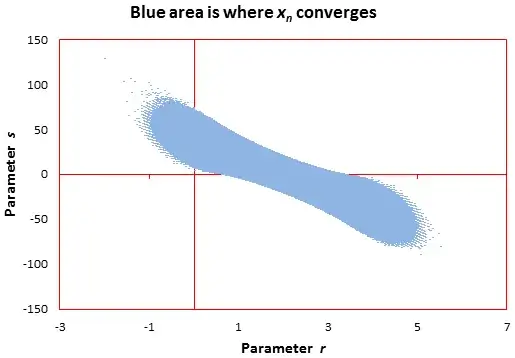
Here we look at the general case, which can be written as: $$2(n+q)x_{n+2}=(r (n+q) + s)x_{n+1} + ((2-r)(n+q)-s)x_n$$

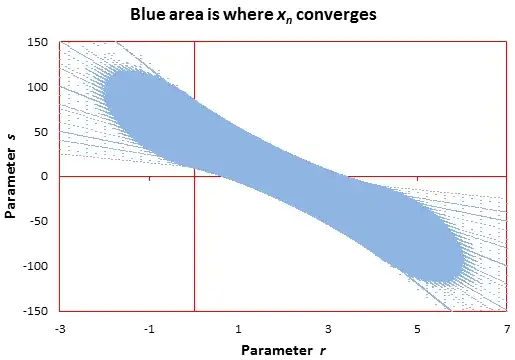
The charts below give some insights about the shape of the convergence regions / boundaries in the full 3-dimensional parameter space.

Case $q=1$:

enter image description here

Case $q=5$:

enter image description here

Time permitting, I will try to create a 3-D picture of the boundary, maybe a rotating one so that it can be viewed under different angles.

Vincent Granville
  • 3,605
  • Why $b_1=b_2-b_3$ ??? – Witold Jan 04 '20 at 12:35
  • Because otherwise if $x_n$ converges, it converges to $0$. There is something wrong in my question: all cases but the first one involve convergence to $0$, precisely because $b_1 \neq b_2 - b_3$. I will fix this. – Vincent Granville Jan 04 '20 at 17:14
  • It is fixed now. I have plenty of other charts, but I want to go through one more round of triple-checking before adding anything else. – Vincent Granville Jan 04 '20 at 17:32
  • You write "Because otherwise if $x_n$ converges, it converges to $0$". It is mistake! It is enough that $a_1=a_2-a_3$, because $(a_1+\frac{b_1}{n})x_{n+2}=(a_2+\frac{b_2}{n})x_{n+1}-(a_3+\frac{b_3}{n})x_{n}$ and $\frac{b_1}{n}$, $\frac{b_2}{n}$, $\frac{b_3}{n}$ are zero as $n \to \infty$. – Witold Jan 04 '20 at 23:34
  • @Witold: No, try $a_3=b_3=0$. Assume $a_1=a_2=1$. Then you have $x_{n+2} = x_1\prod_{k=2}^{n+1} \frac{k-2+b_2}{k-2+b_1}$. If $b_2>b_1>0$ it diverges. If $0<b_2 < b_1$ convergence is to zero (it's a diverging product). Only if $b_2 = b_1$ would it work. But your argument would be correct if instead of $a_i n +b_i$, you use $a_i n^2 + b_i$. – Vincent Granville Jan 05 '20 at 00:03
  • That says, it is a far more complicated problem than I initially thought. I accepted my own answer, but after further investigations, I un-accepted it! – Vincent Granville Jan 05 '20 at 00:07
  • I wrote that I found a mistake in your reasoning. You have not written proof that $b_1=b_2-b_3$. And your reasoning about this contains a logical error. Can you write a complete proof that $b_1=b_2-b_3$? – Witold Jan 05 '20 at 02:26

3 Answers3

1

The representation $2(n+q)x_{n+2}=(r (n+q) + s)x_{n+1} + ((2-r)(n+q)-s)x_n$ is indeed standard, covering all cases where convergence could occur (other than convergence to $0$). The convergence domain for the parameters $q, r, s$ does not depend on $x_0, x_1$ unless $x_0 = x_1$: in that case $x_n=x_0$ for all $n$, regardless of $q, r, s$. I will split my response in two parts: empirical results first, and results based on theory at the bottom.

Empirical results

Below is the convergence domain, in blue, when $q=3.12345$. I will add more cases (other values of $q$) with their corresponding plot. It looks like the shape of the blue area is pretty stable (thought shifted and shrunk or inflated) if $q$ is different. It is not a band as initially thought, but rather a bounded area, and the boundary is a curve. This is not apparent in my original question because I looked at values of $s$ only between $-15$ and $+15$. Here I looked at $s$ between $-150$ and $+150$.

The filaments (and they extend in the central area though it is not visible in the chart below) correspond to annoying cases of convergence, that I would like to exclude. For instance, when all $x_n$ are identical after a fixed number of iterations.

Below is the plot corresponding to $q=3.12345$:

enter image description here

Below is the plot corresponding to $q=5.0918543$ :

enter image description here

Below is the plot corresponding to $q=-0.4539$:

enter image description here

Below is the plot corresponding to $q=-1.4539$:

enter image description here

Below is the plot corresponding to $q=-0.98$:

enter image description here

Below is the plot corresponding to $q=3$:

enter image description here

The cases $q=0, -1,-2, \cdots$ are singular. Also note that the results here were obtained empirically and are subject to machine precision. Increasing machine precision stretches the blue domain, though the shape is unchanged.

Theoretical results

In many cases (see here), $x_{\infty}$ can be expressed as a classic series and the convergence can be studied easily. Most of these series involve only two parameters while our recurrence has three parameters, so it is not sure that the problem can be easily solved entirely based on this strategy, but at least partially for sure.

For instance, $x_n=\sum_{k=0}^{n} \frac{\alpha^k}{k+\beta}$ can be expressed as a recurrence from within our family: $$(n+2+\beta)x_{n+2}=(n(\alpha +1)+\alpha+2+\beta(\alpha+1))x_{n+1}-(n+1+\beta)\alpha x_n$$ and we know convergence occurs if and only if $-1 \leq \alpha < 1$. In this case, $q=\beta+2$ (we assume here that $q \neq 0, -1, -2$ and so on.)

A more general series to consider is the hypergeometric function. Define $x_n$ as the first $n+1$ terms of the series defining that function. This could indeed cover all cases, that is, all values of $q, r, s$. More on this soon.

Exercise: If $q=3, r=-0.4, s = 14.4, x_0=0, x_1=1$, prove that $x_n=1.24$ if $n \geq 2$.

Vincent Granville
  • 3,605
1

Considering $u_n = x_n$ and $v_n = x_{n+1}$ we have the equivalent system

$$ \left( \begin{array}{c} u_{n+1} \\ v_{n+1} \\ \end{array} \right) = \left( \begin{array}{cc} 0 & 1 \\ -\frac{(n+q) r-s}{2 (n+q)} & \frac{(n+q) (2-r)-s}{2 (n+q)} \\ \end{array} \right)\left( \begin{array}{c} u_n \\ v_n \\ \end{array} \right) $$

this system is stable as far as

$$ \text{Eigenvalues} \left( \begin{array}{cc} 0 & 1 \\ -\frac{(n+q) r-s}{2 (n+q)} & \frac{(n+q) (2-r)-s}{2 (n+q)} \\ \end{array} \right) \lt 1 $$

or

$$ \cases{ \left|-\frac{\sqrt{2 (r-6) s (n+q)+((r-12) r+4) (n+q)^2+s^2}+n (r-2)+q (r-2)+s}{4 (n+q)}\right|\lt 1\\ \left|\frac{\sqrt{2 (r-6) s (n+q)+((r-12)r+4) (n+q)^2+s^2}-r (n+q)+2 n+2 q-s}{4 (n+q)}\right|\lt 1 } $$

Cesareo
  • 33,252
0

I decided to add another answer because this one is far more general, far more compact, and covers almost all cases.

Let $$x_n=\sum_{k=0}^n a^kf(k), \mbox{ with } \frac{f(n+2)}{f(n+1)} =\frac{n+c}{n+d}, n\geq 0.$$ We have $$(n+d)x_{n+2}=(n+an+d+ac)x_{n+1}-(na+ca)x_n$$ The standard form being $$2(n+q)x_{n+2}=(r (n+q) + s)x_{n+1} + ((2-r)(n+q)-s)x_n,$$ it follows that $$q=d, r=2(1+a), s=2a(c-d), \mbox{ that is, } a=\frac{r}{2}-1, c=\frac{s}{r-2} +q, d=q.$$ For $n\geq 2$, assuming $x_0=f(0), x_1=f(0)+af(1)$, we also have $$x_n=f(0) + af(1) +af(1) \sum_{k=2}^n\prod_{i=0}^{k-2}\frac{a(c+i)}{d+i}.$$ Thus we have convergence if $|a|< 1$, that is, if $|r-2|<2$. If (say) $a=1$, convergence can occur too, for instance when $d>c+1$. I am going to check why in my previous charts, convergence also seemed to occur with values of $r$ less than $0$.

Note

Some cases of convergence are artificial and must be discarded, in particular if all $x_n$, after a number of iterations, are identical. This happens if for some $n^*$, we have $x_n=x_{n+1}$ if $n\geq n^*$, which happens only when $c=\frac{s}{r-2}$ is a negative integer. This is the case in the exercise at the bottom of my previous answer to this question.

Exercises

Here we assume that $x_0=0$ and $x_1=1$.

  1. If $s=q=0$, prove that $x_\infty = \frac{2}{4-r}$.
  2. If $0<r<2,s<(q+2)(2-r)$ and $q+2>0$, prove that $0< |x_\infty | < 1$.
Vincent Granville
  • 3,605