Is the sum of the reciprocals of primes none of whose proper initial segments are primes converge?
An example of those primes is $88547$, because $8,88,885$ and $8854$ are not primes.
The first few terms in the sequence (A069090) are:
2, 3, 5, 7, 11, 13, 17, 19, 41, 43, 47, 61, 67, 83, 89, 97, 101, 103, 107, 109, 127, 149, 151, 157, 163, 167, 181, 401, 409, 421, 443, 449, 457, 461, 463, 467, 487, 491, 499, 601, 607, 631, 641, 643, 647, 653, 659, 661, 683, 691, 809, 811, 821, 823, 827
The series converges; the limit is approximately $2.48111396244$.
That the series converges follows from the Kraft–McMillan inequality: A uniquely decodable code, and hence in particular a prefix code, satisfies
$$ \sum_ir^{-l_i}\le1\;, $$
where $r$ is the size of the alphabet and $l_i$ is the length of the $i$-th codeword. In the present case, the primes without proper prime prefix form a prefix code $\{q_i\}$ with $r=10$ and $l_i-1\lt\log_{10}q_i$, so
$$ \sum_i\frac1{q_i}=\sum_i10^{-\log_{10}q_i}\le\sum_i10^{-(l_i-1)}\le10\;. $$
The series converges very slowly when summed directly. To compute the limit efficiently, consider the evolution of the set $S\subset[1,10)$ of reals that do not have one of the primes included in the sum so far as a prefix (in decimal notation, without the decimal point). For instance, after excluding $2, 3, 5, 7$ as prefixes, we are left with $S=[1,2)\cup[4,5)\cup[6,7)\cup[8,10)$, and upon excluding the prefix $11$ this is reduced to $S=[1,1.1)\cup[1.2,2)\cup[4,5)\cup[6,7)\cup[8,10)$.
In each range of numbers $\left[10^n,10^{n+1}\right)$ approximately a fraction $\frac1{\log10^n}=\frac1{n\log10}$ of numbers are primes, so on the random model of the primes each such range reduces the measure of $S$ by approximately that fraction. For large $n\gt n_0$, we can approximate the measure $\mu_n$ left in $S$ by integrating the logarithms of the corresponding factors:
\begin{eqnarray} \log\mu_n &\approx& \log\mu_{n_0}+\int_{n_0}^n\log\left(1-\frac1{k\log10}\right)\mathrm dk \\ &\approx& \log\mu_{n_0}-\int_{n_0}^n\frac1{k\log10}\mathrm dk \\ &=& \log\mu_{n_0}-\frac{\log\frac n{n_0}}{\log 10}\;, \end{eqnarray}
so
$$ \mu_n\approx\mu_{n_0}\left(\frac n{n_0}\right)^{-\frac1{\log10}}\;. $$
Thus, the measure of $S$ tends to zero. That means that except for a set of measure $0$, every $x\in [1,10)$ has a prime prefix in decimal notation.
This allows us to compute the desired limit far more efficiently than by directly summing the reciprocals. If a prime $p\in\left[10^n,10^{n+1}\right]$ were to contribute
$$ \int_{\frac p{10^n}}^{\frac{p+1}{10^n}}\frac{\mathrm dx}x=\log\left(1+\frac1p\right) $$
to the sum, then, since all of $[1,10)$ is eventually covered, the limit of the sum would be
$$ \sideset{}{'}\sum_p\log\left(1+\frac1p\right)=\int_1^{10}\frac{\mathrm dx}x=\log10 $$
(where the prime indicates that the sum only runs over the primes without proper prime prefix). Instead, $p$ contributes $\frac1p$, which differs from $\log\left(1+\frac1p\right)$ only on the order of $p^{-2}$. Thus, we have
\begin{eqnarray} \sideset{}{'}\sum_p\frac1p &=& \sideset{}{'}\sum_p\frac1p+\log10-\sideset{}{'}\sum_p\log\left(1+\frac1p\right) \\ &=& \log10+\sideset{}{'}\sum_p\left(\frac1p-\log\left(1+\frac1p\right)\right)\;. \end{eqnarray}
(Note that we're not relying on the specific form $\mu_n\sim n^{-1/\log10}$ estimated above, only on $\lim_{n\to\infty}\mu_n=0$.)
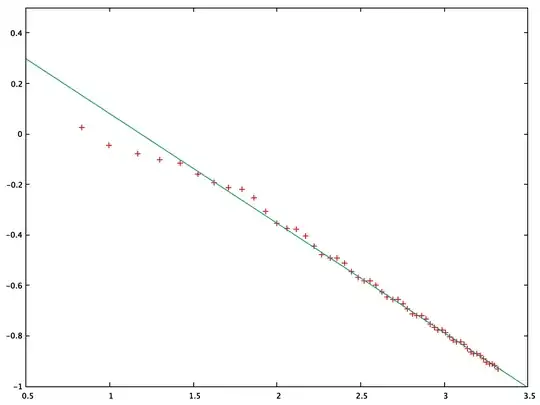
Here's Java code that finds the primes without proper prime prefix and sums $\frac1p$ and $\frac1p-\log\left(1+\frac1p\right)$. The sum of $\frac1p-\log\left(1+\frac1p\right)$ converges to double machine precision with $p\le10^8$; the result (plus $\log10$) is $2.48111396244$. By contrast, with $p\le10^8$ the direct summation of $\frac1p$ only reaches $2.01$. With $p\le10^{12}$, it’s still at $2.09$. Below is a plot of the partial sums of $\frac1p$ for $p\le x$. The abscissa is $\log\log x$; the ordinate is $-\log(S-S(x))$, where $S(x)$ is the partial sum and $S$ is the limit (as determined from the rapidly converging sum). Since the fraction of the sum that's missing at $p\le x=10^n$ is asymptotically proportional to $n^{-1/\log10}\propto(\log x)^{-1/\log10}$, we'd expect this plot to be asymptotic to a line with slope $-\frac1{\log10}$. The green line is a line with that slope fitted to the data. The good agreement of the fit with the data confirms the value of the limit.
