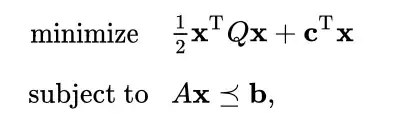1

enter image description here

Does the $\dfrac{1}{2}$ provide any of computation convenience?

Simon Fraser
  • 2,528
Murphy Ho
  • 27
  • 1
    This way, given a quadratic polynomial in several variables, $Q$ is precisely the Hessian matrix of second derivatives. If all coefficients in the polynomial are integers, this way $Q$ has all integer elements. – Will Jagy Dec 31 '19 at 20:48
  • This way, the unconstrained solution is $-Q^{-1}c$ – Bananach Dec 31 '19 at 21:12
  • 3
    You can say it is for computation convenience. Assuming $Q$ is symmetric, the gradient of $x^T Q x$ with respect to $x$ is $2 Qx$. Therefore, $\frac{1}{2}$ constant can cancel the scaling $2$ in the gradient. – user550103 Jan 01 '20 at 08:33
  • Because: https://math.stackexchange.com/q/222894/339790 – Rodrigo de Azevedo Jan 01 '20 at 13:12

0 Answers0