Finding solution for the intersection of a line and and arbitrary-order aspheric lens surface

Question

I apologize for any formatting mistakes, first time here.

I'm currently working on program in Java as a personal project that simulates and allows for the design of a lens system with surfaces generally defined using the equations covered here (Wikipedia). In this case the "order" of the surface referring to the greatest a_xr^x value. Although possible, I'm pretty sure the order rarely is above 12.

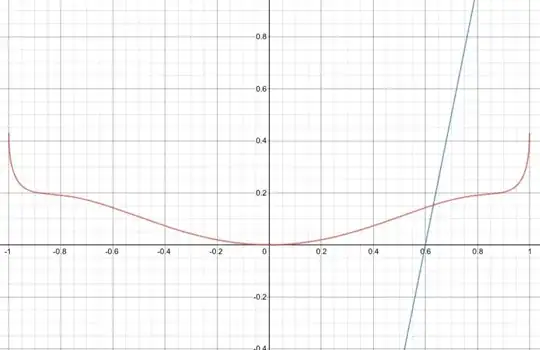
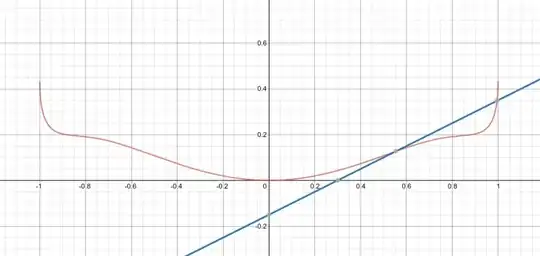
The linked images show two possible cases for a complex aspherical lens defined using this particular equation.

Assuming a "ray" comes from somewhere below the frame upwards as seen in the examples, how would I calculate the first point of collision between that ray and the lens surface? Specifically in three dimensions, as the examples above are only two dimensions as limited by Desmos. Being a lens, the resulting surface in three dimensions is possesses rotational symmetry where the 2D examples have reflection symmetry.

Answer 1

If you want to know the interception point(s) between a surface: $$z = f(x,y)$$ where $f$ is a polynomial of $x$ and $y$ and a ray of light, defined by an equation: $$z = g(x,y)$$ where $g$ is a polynomial of degree $1$ of $x$ and $y$, you can solve an equivalent problem: find the zeros of $$f(x,y) - g(x,y) \ .$$

I.e., let $h(x,y) = f(x,y) - g(x,y)$. When, the values of $x$ and $y$ are such that we have that $h(x,y) = 0$, it means that the value of $f$ (the $z$ coordinate) is equal to the value of $g$ (also the $z$ coordinate).

To find the zeros you may apply Newton's method.

Alternatively, you may follow the ray of light and, using successive bisections, try to find the "smallest" zero. However, the first zero you find may be close or far away from the "smallest" zero, so you need to be prepared for that case.