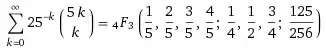On sums such as $\sum_{k=0}^\infty \binom{2k}{k}\frac{1}{8^k}=\sqrt{2}$

Question

This identity is a special case of a more general formula found here, and known at least since 1972 (published in Abramowitz and Stegun 1972, p. 555.) Many remarkable series involving the inverse of binomial coefficients are known and listed in the same source, see also here for a way to derive them.

However, there are plenty of interesting series involving binomial coefficients (not their inverse) that are not listed in the references that I checked. For instance:

$$\sum_{k=0}^\infty \binom{3k}{k}\frac{1}{8^k}=\frac{4\sqrt{10}}{5}\cos\Big(\frac{1}{3}\arcsin \frac{3\sqrt{6}}{8}\Big)$$

$$\sum_{k=0}^\infty \binom{4k}{2k}\frac{1}{32^k}= \sin\frac{\pi}{8}+\cos\frac{\pi}{8}$$

Another example is:

Question

How do you prove these results? I found them using WolframAlpha symbolic calculator, see here for an example. One of these results is proved here, but I am looking for a proof that would apply to a broad class of such series.

Background

The reason that I am interested in powers of two ($8^{-k}, 32^{-k}$) is because I am looking for series converging to irrational numbers, with each term being a fraction: the denominator is a power of two, and the numerator is an integer (a binomial coefficient in this case.) The goal is to gain some insights in the binary digit distribution of numbers such as $\sqrt{2}$.

For instance, a result that could be useful for me is the following:

$$\sqrt{2} = \lim_{n\rightarrow\infty}\frac{P_n}{8^n} = \lim_{n\rightarrow\infty}\frac{1}{8^n}\sum_{k=0}^n 8^{n-k}\binom{2k}{k},$$ with $P_n$ being an integer.

Answer 1

The Lagrange Inversion Formula provides an appropriate method to derive \begin{align*} \sum_{k=0}^\infty \binom{3k}{k}\frac{1}{8^k}=\frac{4\sqrt{10}}{5}\cos\Big(\frac{1}{3}\arcsin \frac{3\sqrt{6}}{8}\Big)\tag{1} \end{align*}.

Let a formal power series $w=w(t)$ be implicitely defined by a relation $w=t\Phi(w)$, where $\Phi(t)$ is a formal power series such that $\Phi(0)\ne0$. The Lagrange Inversion Formula (LIF) states that:

$$[t^n]w(t)^k=\frac{k}{n}[t^{n-k}]\Phi(t)^n$$

A variation stated as formula $G6$ in Lagrange Inversion: when and how by R. Sprugnoli (etal) is:

Let $F(t)$ be any formal power series and $w=t\Phi(w)$ as before, then the following is valid:

\begin{align*} [t^n]F(t)\Phi(t)^n=\left[\left.\frac{F(w)}{1-t\Phi'(w)}\right|w=t\Phi(w)\right]\tag{2} \end{align*}

Note: The notation $[\left.f(w)\right|w=g(t)]$ is a linearization of $\left.f(w)\right|_{w=g(t)}$ and denotes the substitution of $g(t)$ to every occurrence of $w$ in $f(w)$ (that is, $f(g(t))$). In particular, $w=t\Phi(w)$ is to be solved in $w=w(t)$ and $w$ has to be substituted in the expression on the left of the $|$ sign.

In order to prove (1) we set $F(t)=1$ and $\Phi(t)=(1+t)^3$. We then have

$$t\Phi'(w)=3t(1+w)^2=\frac{3t\Phi(w)}{1+w}=\frac{3w}{1+w}$$

It follows:

\begin{align*} \binom{3n}{n}&=[t^n]F(t)\Phi(t)^n=[t^n](1+t)^{3n}\\ &=[t^n]\left[\left.\frac{1}{1-t\Phi'(w)}\right|w=t\Phi(w)\right]\\ &=[t^n]\left[\left.\frac{1}{1-\frac{3w}{1+w}}\right|w=t\Phi(w)\right]\\ &=[t^n]\left[\left.\frac{1+w}{1-2w}\right|w=t\Phi(w)\right]\\ \end{align*} Let \begin{align*} A(t):=\sum_{n\ge0}\binom{3n}{n}t^n=\left.\frac{1+w}{1-2w}\right|_{w=t\Phi(w)} \end{align*}

Expressing $A(t)=\frac{1+w}{1-2w}$ in terms of $w$, we get

$$w=\frac{A(t)-1}{2A(t)+1}$$

Since $w=t\Phi(w)=t(1+w)^3$, we obtain \begin{align*} \frac{A(t)-1}{2A(t)+1}=t\left(1+\frac{A(t)-1}{2A(t)+1}\right)^3 \end{align*}

which simplifies to: \begin{align*} (4-27t)A(t)^3-3A(t)-1=0\tag{3} \end{align*}

In order to get the RHS of $(1)$ we first analyse the structure of (3) which is

$$f(t)A(t)^3-3A(t)=1$$

with $f(t)$ linear and observe a similarity of this structure with the identity

$$4\cos^3{t}-3\cos{t}=\cos{3t}$$

Thus we use the ansatz:

\begin{align*} A(t) := \frac{2\cos\left(g(t)\right)}{\sqrt{4-27t}}\tag{4} \end{align*}

We see

\begin{align*} (4-27t)A(t)^3-3A(t) &=\frac{8\cos^3\left(g(t)\right)}{\sqrt{4-27t}}-\frac{6\cos\left(g(t)\right)}{\sqrt{4-27t}}=\\ &=\frac{2\cos\left(3g(t)\right)}{\sqrt{4-27t}}\\ &=1 \end{align*}

Now, since

\begin{align*} 2\cos\left(3g(t)\right)&=\sqrt{4-27t}\\ 4\cos^2\left(3g(t)\right)&=4-27t\\ \sin^2\left(3g(t)\right)&=\frac{27}{4}t\\ \end{align*}

we get \begin{align*} g(t)&=\frac{1}{3}\arcsin\left(\frac{3\sqrt{3t}}{2}\right)\tag{5}\\ \end{align*}

We finally conclude from (4) and (5) \begin{align*} \color{blue}{\sum_{k=0}^\infty \binom{3k}{k}\frac{1}{8^k}} &=\left.\frac{2\cos(g(t))}{\sqrt{4-27t}}\right|_{t=\frac{1}{8}}\\ &=\left.\frac{2\cos\left(\frac{1}{3}\arcsin\left(\frac{3\sqrt{3t}}{2}\right)\right)}{\sqrt{4-27t}}\right|_{t=\frac{1}{8}}\\ &\,\,\color{blue}{=\frac{4\sqrt{10}}{5}\cos\left(\frac{1}{3}\arcsin\left( \frac{3\sqrt{6}}{8}\right)\right)} \end{align*} and the claim follows.

Answer 2

The binomial theorem can famously prove such sufficiently-small-$x\ge0$ results as$$\sum_{k\ge0}\binom{2k}{k}x^k=(1-4x)^{-1/2}$$(which is useful in deriving the $n$th Catalan number from their generating function) and$$\sum_{k\ge0}\binom{4k}{2k}x^k=\frac{(1-4\sqrt{x})^{-1/2}+(1+4\sqrt{x})^{-1/2}}{\sqrt{2}}$$(this is just the even-$k$ terms of the first result, i.e. the function's even part, after we replace $x$ with $\sqrt{x}$).

I had to resort to WA for$$\sum_{k\ge0}\binom{3k}{k}x^k=\left(1-\frac{27}{4}x\right)^{-1/2}\cos\left(\frac13\arcsin\sqrt{\frac{27x}{4}}\right),$$which can be rewritten with more complicated radicals using$$c:=\cos\left(\frac13\arcsin\sqrt{\frac{27x}{4}}\right)\implies4c^3-3c=1-\frac{27x}{4}.$$If you get such a form using Cardano's method (but I should mention that kinda misses the point), you can use the binomial theorem to prove it. This illustrates the benefits of a hybrid use of EESs: get the answer from them, then prove it with some inspiration.

But $\sum_{k\ge0}\binom{5k}{k}x^k$ didn't, in WA's opinion, succumb to the same analysis, which is why you'd need the suggestion of @LordSharktheUnknown's first comment to get the hypergeometric result (the last argument generalises to $\frac{5^5x}{4^4}$).

Answer 3

Another way is to use the integral representation of the binomial coefficient $$\dbinom{n}{k}=\frac{1}{2\pi i}\oint_{|z|=1}\frac{\left(1+z\right)^{n}}{z^{k+1}}dz.$$ For example we have $$\sum_{k\geq0}\frac{1}{8^{k}}\frac{1}{2\pi i}\oint_{\left|z\right|=1}\frac{\left(1+z\right)^{2k}}{z^{k+1}}dz=\frac{1}{2\pi i}\oint_{\left|z\right|=1}\frac{1}{z}\sum_{k\geq0}\frac{1}{8^{k}}\frac{\left(1+z\right)^{2k}}{z^{k}}dz$$ $$=-\frac{1}{2\pi i}\oint_{\left|z\right|=1}\frac{8}{z^{2}-6z+1}dz$$ and since we have a pole at $z=3-2\sqrt{2}$ we get $$\sum_{k\geq0}\frac{1}{8^{k}}\dbinom{2k}{k}=\color{red}{\sqrt{2}}.$$ In a similar way $$\sum_{k\geq0}\frac{1}{8^{k}}\frac{1}{2\pi i}\oint_{\left|z\right|=1}\frac{\left(1+z\right)^{3k}}{z^{k+1}}dz=-\frac{1}{2\pi i}\oint_{\left|z\right|=1}\frac{8}{z^{3}+3z^{2}-5z+1}dz$$ and since we have a pole at $z=\sqrt{5}-2$ we get $$\sum_{k\geq0}\frac{1}{8^{k}}\dbinom{3k}{k}=\color{red}{1+\frac{3}{\sqrt{5}}}.$$