I have tried a lot but i do not seem to find an equation. Question is the following:
Find an equation of the specified curve, that is, of the locus of points the sum of whose distances from the points $(2,3)$ and $(4,1)$ is $8$.
I first tried to translate and rotate the axis to see the ellipse like its center lies on the origin $(0,0)$. It seemed to be tough. I know I can use the general equation with center $(h,k)$ but then there will not be any rotation though the major axis is rotated.
An ellipse is the geometric place of the points $P(x,\,y)$ of the plane for which the sum $d > 0$ of the distances from two fixed points $F_1(x_1,\,y_1),\,F_2(x_2,\,y_2)$, called foci, remains constant:
$$ \sqrt{(x-x_1)^2+(y-y_1)^2} + \sqrt{(x-x_2)^2+(y-y_2)^2} = d\,. $$
Manipulating this equation we obtain the Cartesian equation of the desired ellipse.
Algorithmically, given two points $F_1(x_1,\,y_1),\,F_2(x_2,\,y_2)$ and a number $d > 0$, if: $$ \Delta := d^2 - (x_1-x_2)^2 - (y_1-y_2)^2 > 0 $$ then an ellipse of parametric equations was identified: $$ (x,\,y) = (A + B\,\cos\theta + C\,\sin\theta, \; D + E\,\cos\theta + F\,\sin\theta)\,, \; \; \; \text{with} \; \theta \in [0,\,2\pi) $$ where: $$ \begin{aligned} & A = \frac{x_1 + x_2}{2}\,, \; \; \; B = \frac{\sqrt{\Delta + \left(x_1-x_2\right)^2}}{2}\,, \; \; \; \; \; C = 0\,, \\ & D = \frac{y_1 + y_2}{2}\,, \; \; \; E = \frac{\left(x_1-x_2\right)\left(y_1-y_2\right)}{4\,B}\,, \; \; \; F = \frac{d\,\sqrt{\Delta}}{4\,B}\,. \end{aligned} $$
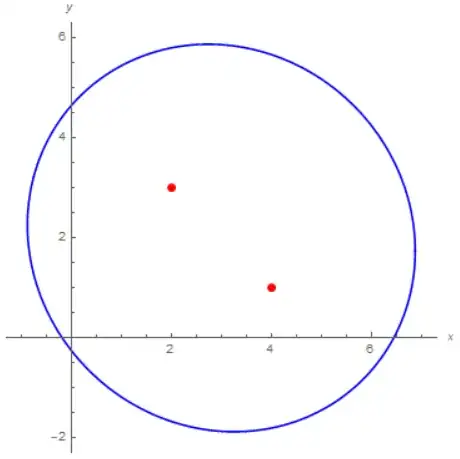
Specifically, being $(x_1,\,y_1)=(2,\,3)$, $(x_2,\,y_2)=(4,\,1)$ and $d = 8$:
I don't know. For problems like this, I just use the distance formula and grind through the algebra. (Then double-check my solution against Wolfram Alpha.)
$$\sqrt{(x-2)^2+(y-3)^2}=8-\sqrt{(x-4)^2+(y-1)^2}\\ (x-2)^2+(y-3)^2=64+(x-4)^2+(y-1)^2-16\sqrt{{(x-4)^2+(y-1)^2}}\\ (x^2-4x+4)+(y^2-6y+9)=64+(x^2-8x+16)+(y^2-2y+1)-16\sqrt{{(x^2-8x+16)+(y^2-2y+1)}}\\ 4x-4y-68=-16\sqrt{x^2+y^2-8x-2y+17}\\ x-y-17=-4\sqrt{x^2+y^2-8x-2y+17}\\ (x-y-17)^2=16(x^2+y^2-8x-2y+17)\\ x^2+y^2+289-2xy-34x+34y=16x^2-128x+16y^2-32y+272\\ 15x^2+2xy+15y^2-94x-66y-17=0 $$
Let the distances to the foci be $d_1,d_2$ and their sum be $d$. We have
$$d=d_1+d_2$$
Squaring,
$$d^2-d_1^2-d_2^2=2d_1d_2.$$
Squaring a second time,
$$d^4-2d^2(d_1^2+d_2^2)+(d_1^2+d_2^2)^2=4d_1^2d_2^2,$$
or
$$d^4-2d^2(d_1^2+d_2^2)+(d_1^2-d_2^2)^2=0.$$
Expanding the distances, we have
$$d_1^2+d_2^2=2x^2+2y^2-2(x_1+x_2)x-2(y_1+y_2)y+x_1^2+x_2^2+y_1^2+y_2^2\\ =2x^2+2y^2-2\sigma_xx-2\sigma_yy+\Sigma$$
and
$$d_1^2-d_2^2=-2(x_1-x_2)x-2(y_1-y_2)y+x_1^2-x_2^2+y_1^2-y_2^2\\ =-2\delta_xx-2\delta_yy+\Delta,$$
and
$$(d_1^2-d_2^2)^2=4\delta_x^2x^2+8\delta_x\delta_yxy+4\delta_y^2y^2-4\delta_x\Delta x-4\delta_y\Delta y+\Delta^2.$$
Finally, we get the conic
$$4(\delta_x^2-d^2)x^2+8\delta_x\delta_yxy+4(\delta_y^2-d^2)y^2-4(\delta_x\Delta+d^2\sigma_x) x-4(\delta_y\Delta+d^2\sigma_y)y\\ +\Delta^2-2d^2\Sigma+d^4=0.$$
Check:
With the usual placement of the foci, $(f,0)$ and $(-f,0)$, we have $\sigma_x=\sigma_y=\delta_y=\Delta=0$, $\delta_x=2f$ and $\Sigma=2f^2$. The equation reduces to
$$4(d^2-4f^2)x^2+4d^2y^2=d^2(d^2-4f^2).$$
You write that you had considered a general ellipse equation with center somewhere other than the origin, but there was no rotation involved. It sounds to me like your “general” equation wasn’t general enough. Including an axis rotation, a general equation for an ellipse has the form $${((x-h)\cos\theta+(y-k)\sin\theta)^2\over a^2}+{(-(x-h)\sin\theta+(y-k)\cos\theta)^2\over b^2} = 1. \tag1$$ Now, the semimajor axis length $a$ is half of the constant distance to the foci, and for the semiminor axis length we have $b^2=a^2-c^2$, where $c$ is half the distance between the foci, so finding the two denominators is easy. The center $(h,k)$ is the midpoint of the foci, so that’s easy, too. For the major axis rotation angle $\theta$, you just need to find the slope of the line through the foci, which is $\tan\theta = {1-3\over4-2}=-1$, so you can take $\theta=-\pi/4$. In this case, $\tan\theta$ turned out to be one of the commonly-known values, so computing $\theta$ was easy, but observe that you don’t really need to know the angle $\theta$ explicitly to form equation (1): you need its sine and cosine, both of which can be computed from the tangent, to wit, $$\cos^2\theta = {1\over\tan^2\theta+1} = \frac12 \\ \sin^2\theta = \cos^2\theta\tan^2\theta = \frac12.$$ Choose the signs of the square roots so that $\tan\theta$ has the correct sign. Of course, we could’ve skipped computing $\tan\theta$ first and gotten the sine and cosine directly from the coordinates of the foci.
Equation (1) can be hard to remember—I always have to reconstruct it to make sure that I’ve gotten the signs right. However, observe that $-(x-h)\sin\theta+(y-k)\cos\theta=0$ is the equation of a line through $(h,k)$ with slope $\tan\theta$, i.e., it’s the major axis. Similarly, $(x-h)\cos\theta+(y-k)\sin\theta=0$ is an equation of the minor axis. I usually just work out the equations of these lines, normalize them, and then plug them in for $x$ and $y$ in the standard equation ${x^2\over a^2}+{y^2\over b^2}=1$.
