2

I checked existing questions but couldn't find the case I wanted.

I have a set of tiles of known relative size. The tiles could be squares, circles, or rectangles. They all have the same aspect ratio but different relative areas, like one might be 2.3x larger than another, etc.

I am trying to draw these as large as possible into a rectangle of known size. The rectangle could have an arbitrary aspect ratio.

I can do it easily if all of the tiles are the same size, but not sure where to start with different sizes.

For example, imagine a channel guide, where I know the relevance of each channel to the viewer. I want to have a preview of each channel as a 16:9 rectangle. I want the size of the rectangle to reflect it's relevance. I want these to fill the screen as much as possible. The screen could be a 4:3 monitor or a 9:16 phone.

Note that it is not required that the tiles exactly fill the container - just trying to get as close as possible.

Any help would be appreciated.

Dave Vronay
  • 121
  • Can you clarify the problem a bit? Give an example. If you only care about bounding boxes remove all talk of squares and circles. Here is an example as I understood it: "Suppose I have 3 tiles all with aspect ratio1:2, with relative sizes 1, 2, 3. Given some rectangle, how can I fit all three rectangles inside, keeping their relative size, and maximizing their area?"

    These types of problems are extremely hard, if you want this for a practical application, you may also want to add what types of compromises you can live with as an exact solution is unlikely.

     – Herman Tulleken Dec 21 '19 at 00:24
  • For example, imagine a channel guide, where I know the relevance of each channel to the viewer. I want to have a preview of each channel as a 16:9 rectangle. I want the size of the rectangle to reflect it's relevance. I want these to fill the screen as much as possible. The screen could be a 4:3 monitor or a 9:16 phone. – Dave Vronay Dec 22 '19 at 12:35
  • The example makes it clearer :); add it to your question so other people can see it easier. – Herman Tulleken Dec 22 '19 at 13:17

2 Answers2

1

Short answer: in general there is no solution to your problem. Below I explain this a bit, and give some possible ideas for compromises.

Ok, let's assume that all aspect ratios are the same (the tiles and the region to be tiled.) For simplicity, let's work with a square (you can stretch the solution afterward to the correct aspect ratio.)

The problem is now to find tiling of a square using $n$ squares, with areas given (really, their relative areas are given, but since they must sum to the area of the big square, we can work out what they are.)

It is known that a square cannot be tiled by 2, 3, or 5 squares. (It is not too hard to prove for 2 and 3, not so sure about 5; you can give it a go.) For 4 squares, there is only one layout: all the squares are the same size (so you cannot present channels with different importance using this scheme if there are only 4).

There is a layout for any number of squares if there are 6 or more. (See my answer here that proves that.)

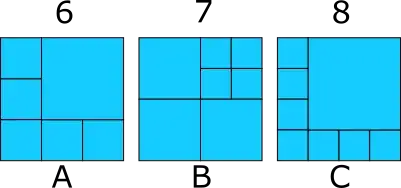
In general there are several possibilities for each $n$, but we cannot match arbitrary areas. For example, the solution for 6 squares we must have 5 squares that have area $1/4$ of the big square. For 10 squares, there are these two schemes. (I haven't verified that these are the only ones but I think so).

enter image description here

In any case, so for $n$ you have a few possible layouts; how do you decide which to use?

Simple ranking: In this scheme, you maximize the variance in square sizes, and then simply assign the biggest channel to the biggest square, and so on. To maximize the variance in square sizes, follow this algorithm:

Start with one of the following layouts depending on value of $n \bmod 3$ (the first if it is 0, the second if it is 1, the third if it is 2). Keep dividing the smallest square into 4 until you have enough total squares.

Optimization Algorithm: In this scheme, you will find the "best" solution in some sense. However, you first need to define what the "best" means for you.

One way to do it is to define an error value for a layout:

$E = \sum_i (a_i - c_i)^2,$

where $a_i$ is the actual area you want, and $c_i$ is the area of the square in the layout you assign to represent it (again, you can match biggest squares to biggest channels). You can then choose the layout scheme that minimizes this value.

This will require you to find all possible layouts for a given $n$. An algorithm for this is to find tilings of squares by squares of size $1, 2, ..., \lceil\sqrt{n}\,\rceil$ and reject solutions that use the wrong number of squares. This may be unfeasible for very large $n$, and slow even for smaller $n$. You would probably need to make a database of solutions so you dont have to generate them each time (although I have no idea how many there are; space may become the next problem).

Best of $k$ guesses: An alternative is to generate $k$ randomish solutions using the scheme I described under ranking, but instead of choosing the smallest square each time, you choose a random one. This algorithm is very fast, so you can generate 100 (or a 1000) quickly, and select the best one using the error. (Since it will be an approximation in any case, this will be more than enough accuracy for your use case.) This is the solution I would use in the real world.

Herman Tulleken
  • 3,608
  • I like this approach - especially keeping track of the errors. One thing I should clarify if it wasn't obvious is that it is not required that tiles exactly cover the container. I am assuming that is not typically possible. So - getting as close as possible is the goal. Measuring error is a good one. – Dave Vronay Dec 23 '19 at 02:02
  • @DaveVronay Ah that changes the problem completely. I leave this answer here for someone else that finds this question and may find it useful, but I gave a separate answer that may be more useful to you. – Herman Tulleken Dec 24 '19 at 04:53
1

If you do not need to cover the entire region with your tiles, we can reduce the problem of finding the smallest square that will fit a set of squares with given areas. (The areas are proportional to what you want them to represent. Once you have a solution you scale everything to fit your region you want to pack; this will be the tightest packing.

With this formulation you will probably be able to find a lot of literature, using search terms like "square packing". Here is a problem trying to find the smallest rectangle that will fit a number of squares. (This can already be used in an algorithm; see below). (Unfortunately, this area seems to be dominated by a very specific (and different) problem, so you will have to wade through a lot of papers to get what you want.) Here is another related paper.

From the literature, you will find state-of-the-art algorithms. Below I give a naive algorithm that may be a good starting point for a practical application. (I am a big fan of implementing a vanilla algorithm as a benchmark, even if it is too slow for production software, because papers describing fancy algorithms are often vague in important details, or have mistakes that are hard to uncover, so getting towards a correct implementation can be very time-consuming. A benchmark makes it much faster to check correctness.)

First, make your problem discrete by deciding on a suitable unit (not too fine) that you can use so that all squares have integer coordinates.

Then, find a square that will definitely fit all your squares. (Using the dimensions of the minimum rectangle in the first paper I linked will give you such a square, taking the longest dimension of the rectangle to use for the square size.)

Now iterate over the square size downwards and see if (using a simple back-track algorithm), you can find tighter packings. Stop once you checked the last square that has an area bigger than the sum of the tiles.

This may work quite well for grid-sizes $10 \times 10$ to $20\times 20$. You can try other schemes to find a solution fast (skipping over square sizes, using lower res to establish bounds faster, etc.).

Herman Tulleken
  • 3,608