Consider $\max\{xy:(x,y) \in M \}$ with the set $M := \left \{ (x,y) \in \mathbb{R}^2: x^2+y^2 \leq 4\right \} $
How or where do I have to sketch the level sets $N_c = \{(x,y) : xy = c \}$ for $c =0$, $c=1$, $c=4$ and $M$?
When I write $x^2+y^2 = c$ in Desmos I get this for
$c=1$
and this for
$c=4$
For $c=0$ I get nothing and regarding $M$ I don't know how it's done. Is $M$ just a circle $<= 4$?
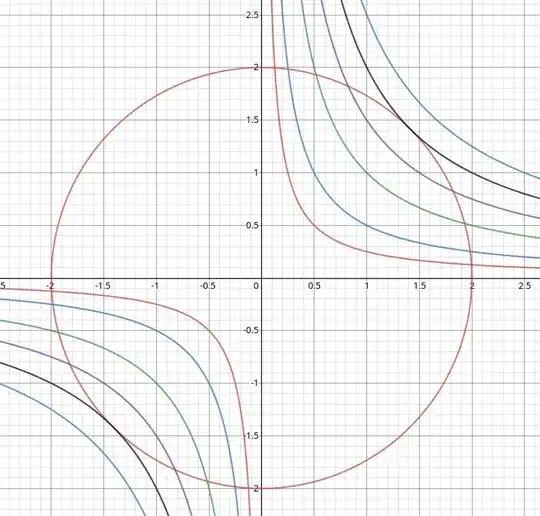
These are the level sets $xy = c$ for $c \in \{\frac14, \frac12, 1, \frac32, 2, \frac52\}$:
Interactive version: https://www.desmos.com/calculator/geop2hyhgv
The point of the level curves is to demonstrate two things:
If the maximum of $xy$ is $c^*$ that means there exists points $x^*, y^*$ on the curve $x^2 + y^2 = 4$ such that $x^*y^* = c^*$. This means that $(x^*, y^*)$ is a solution to both $x^2 + y^2 = 4$ and $xy = c^*$. In particular, the two curves $x^2 + y^2 = 4$ and $xy = c^*$ intersect.
The maximum of $xy$ is the largest $c$ for which the curves $xy = c$ and $x^2 + y^2 = 4$ intersect. Notice in the picture that $xy = c$ intersects the circle if $|c| \le 2$ but, for instance, $xy = \frac52$ does not intersect the circle.
When we take $c = c^* = 2$, the curve $xy = 2$ is tangent to the curve at the intersection point(s) $(x^*, y^*) = (\pm \sqrt2, \pm \sqrt2)$. It is this observation that allows us to solve the problem using calculus.
The gradient of $x^2 + y^2$ is $(2x, 2y)$. The gradient of $xy$ is $(y,x)$. For the curves $x^2 + y^2 = 4$ and $xy = c$ to be tangent, the gradients should be parallel. This gives us the Lagrange condition $$(2x, 2y) = \lambda(y,x).$$ The solutions to this are $y = \pm x$ (and $\lambda = \pm 2$, but that's unimportant). I know, from plotting the level curves that $y = x$ will give the maximum and $y = -x$ will give the minimum. If we pretend that we don't know this, then we need to substitute $y = \pm x$ into the curve we know: $x^2 + y^2 = 4$ (we don't yet know what $c$ is so substituting into $xy = c$ doesn't help). This gives $2x^2 = 4$ and $x = \pm \sqrt 2$. Then we check $x = \pm \sqrt 2$ and $y = \pm x$ to find the mins and maxes.
HINT
You are looking to maximize $xy$ over the circle of radius 2, centered at the origin. It is easy to see that the maximum will occur on the boundary, where you have $x^2+y^2=4$.
Now you can either apply Lagrange multipliers or solve for $y = \pm \sqrt{4-x^2}$ and apply symmetry, optimizing the one-variable function $f(x, y(x)) = x\sqrt{4-x^2}$.
More formally, you have to consider the function $f(x,y)$ for relative extrema which amounts to solving $\frac{\partial f}{\partial x} = 0 = \frac{\partial f}{\partial y}$. Note that $\frac{\partial f}{\partial x} = y$ and $\frac{\partial f}{\partial y} = x$, so the system yields $x=y=0$, which is obviously not a maximum point.
Note that $|xy| \leq |x| |y|$ and $x^2+y^2=|x|^2+|y|^2$ so that the maximum is attained at some $x,y\geq 0$. Now, by AM-GM, for $x,y\geq 0$, we have $$xy=\sqrt{x^2y^2} \leq \frac{x^2+y^2}{2} = 2,$$ with equality for $x=y$. It follows that $x=y=\sqrt{2}$ is a maximizer. To find the other maximizers, you need to find all the real solutions of $x^2=2$.
