6

Problem:

There are $2$ concentric circles in a plane. $3$ points are on the circumference of the inner circle and $6$ points are on the outer circle. Each of these points is joined to every one of the remaining $8$ points. What is the minimal number of lines formed from these $9$ points?

At first I believed the answer is $21$ with the following construction (figure 1): Choose $3$ arbitrary points $B_1, B_2, B_3$ on the inner circle. Connect them and extend the lines to intersect the outer circle at $6$ points $A_1, A_2, A_3, A_4, A_5, A_6$. $3$ lines each pass through $4$ points; every other line passes through $2$ points. It can be counted that the total number of lines is $$\binom{9}{2}-3\Big(\binom{4}{2}-1\Big)=21.$$

I tried to prove that $21$ is the minimum using calculations but without success. I later found another more complicated construction with fewer lines (figure 2):

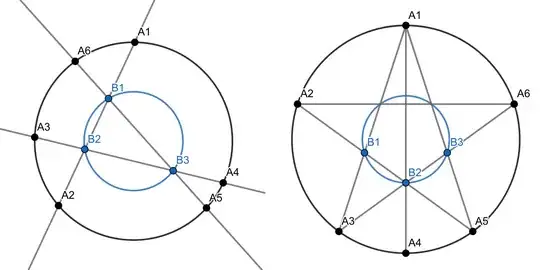solutions (Not all lines are drawn in the figures.)

$2$ lines each pass through $4$ points; $3$ lines each pass through $3$ points; every other line passes through $2$ points. The number is $$\binom{9}{2}-2\Big(\binom{4}{2}-1\Big)-3\Big(\binom{3}{2}-1\Big)=20.$$

My question is that can the answer $20$ be further improved? If not, how can I verify that $20$ is the minimum?

Community
  • 1
Wang Weixuan
  • 470

1 Answers1

2

A general expression for N points could be obtained by considering the secant function. The secant function is the tangent of both hyperbolic sine and cosine functions, which will be the phase space for something called saturation when considering concentric circles. Abstractly, this kind of question is related to things called k-rich lines, which is a geometry of separation nodes when mixing functions. There are two answers, one for $ r $ being the inner circle and $ r_0 $

This is what you have been counting in the form of a power series:

$$ r \sec(\theta_{2} - \theta_{1}) = r_{0} $$

$$ r = r_{0} + a \cdot t $$

$$ r - r_{0} = a \cdot t $$

$$ h(t) = \Sigma_{n=1}^{\infty} a_{n}t^{n} $$

as the step function within the matrix $ a \cdot t $

$$ s = r \theta $$

$$ s_{2} - s_{1} = ds $$

as a metric of curvature, giving convex or concave solutions.

$ ds = dr + dt $ using operator calculus $ \frac{ds}{dr} = \frac{dt}{dr} $

and $ \frac{ds}{dt} = \frac{dr}{dt} $ with $\frac{dr}{ds} = -\frac{dt}{ds} $

From here we can see that the curvature is reflexive between radius and time, and that the radius and curvature are linear with the curvature and time. As the latter is a tautology we can focus on the reflexive relationship and gain a linear solution to the power series.

So $ r - t = -r $ rearranging we get $ 2r = t $ and $ r = \frac{t}{2} $

$ a $ is then a coefficient that defines the distance between points, with the dimension it resides in being the number of points, and $ t $ is a parameter that defines the number of lines that you draw with those points. The is the nature of the power series when dealing with questions when the answer is infinity.

Define these are matrices of whatever dimension you wish for $ a $ and the saturation matrix $ t $ and compute their scalar product $ a \cdot t $ to find the crossings.

So in general the equation then becomes:

$$ (a + t)^{n} = \binom{n}{m} t^{n} a^{n-m} $$

a simple binomial distribution for dimension $ n $ and curvature $ m $ we have $ |n \times m| \leqslant k $ where k is the separation of the two circles.

Fun fact: this is the exact method Isaac Newton used with his optic rings to deduce that binomial series exist.

Wang Weixuan
  • 470