I have an N-body simulation. Each body in the simulation has an array of positions as a function of time. For example, the body Earth has the following positional coordinates (in meters) over 10 years (using time-step of 2 days):
.. body: Earth
[[ 1.50124878e+11 -8.10072107e+09 0.00000000e+00]
[ 1.49423093e+11 5.14365190e+09 0.00000000e+00]
[ 1.49069175e+11 1.02812108e+10 0.00000000e+00]
...
[ 1.49035495e+11 -1.83159842e+10 0.00000000e+00]
[ 1.49667650e+11 -1.32192204e+10 0.00000000e+00]
[ 1.50124878e+11 -8.10072107e+09 0.00000000e+00]]
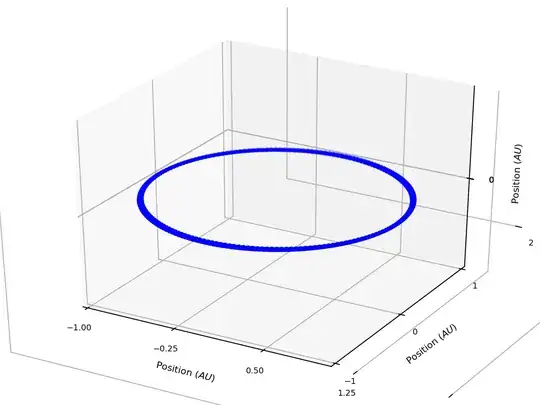
The shape of this array is (1826, 3); that is, 3 position-vector components (x, y, z) taken over 1826 different times. In position-space (for which each scattered point represents the position at a unique time), this looks like:
Since I know the shape is an ellipse in the xy-plane, I can fit the ellipse directly. By fit, I mean find the optimal parameters that minimize some error function (like least squares). For the general conic section in the xy-plane, the formula of the generalized conic (discussed in this post) is: $^2++^2+++=0$
But, what if I can find a body for which the z-components of the positional vector are not constant (at f=0)? In this case, fitting the conic section now becomes more difficult (conceptually for me, but also computationally). One solution I've seen briefly mentioned online is to use dimensionality reduction; ie, reduce the data from a 3-d dataset to a 2-d dataset.
I am not sure, but I think that the best way to go about reducing the last dimension of data would be to find the proper rotation matrix such that the z-components of the rotated position vector will be a constant (if the data will allow for it); then, I can use the general conic formula (linked above). If this idea makes sense, then how does one go about finding this rotation matrix? If this idea is nonsense, how does one go about fitting the conic section to 3-d points?