1

I'm trying to solve a quintic equation for $y$ in terms of $x$ and $z$ where $x,y,z\in\mathbb{N}$ and correct combinations of $z,x$ will yield a $\textbf{positive}$ integer $y$.

$$2 x^5 y + 10 x^4 y^2 + 20 x^3 y^3 + 20 x^2 y^4 + 8 x y^5 - z = 0$$

I've read books that helped a little (including "Beyond the Quartic Equation") but my math background is not strong about groups, symetry and the like. On a lark, I asked Wolfram and it gave me results I don't understand. Disregarding the complex solutions:

Why is it negative, what is $F_3$, and what is represented by the quotients in parentheses?

$$y = -\frac{2 z _4 F_3(1/5, 2/5, 3/5, 4/5;1/2, 3/4, 5/4;\frac{3125 z^4}{x^24})}{x^5} - x/2$$

Is Wolfram's answer useful? Where should I go from here?

poetasis
  • 6,338
  • 1
    This is called "generalized hypergeometric function" ${_4F_3}$, wikipedia article on them is quite good – Yuriy S Dec 14 '19 at 18:22
  • I tried looking up hypergeometric stuff before but I don't understand it and I don' see how it would apply. I will know the discrete values of $z$ and, for each, I will know a range of values for $x$. I'm looking for a solution where, for example $f(z,x): f(60,1)=1, f(780,1)=2, f(12180,2=2), f(595140,4)=3$ etc. – poetasis Dec 14 '19 at 18:37
  • I think using the Diophantine equation solver would be more helpful, at least if you just looking to see if you can find any solutions, without worrying about whether you have found all of them. – Dave L. Renfro Dec 14 '19 at 18:40
  • @Dave L. Renfro I looked at the link but it showed negative values of $x$ and zero values for $z$ which will never be the case. I will know $\textbf{all}$ values of $z$ to be used and all ranges of $x$ to be used in finding integers $y$. – poetasis Dec 14 '19 at 19:34

1 Answers1

2

Not an answer, but I hope it clears some things. (See the last part especially).

First of all, we can simplify the equation by introducing $y=xt$, then we obtain:

$$x^6(2 t + 10 t^2 + 20 t^3 + 20 t^4 + 8 t^5) - z = 0$$

$$4t^5+10t^4+10t^3+5t^2+t= \frac{z}{2 x^6}$$

Let's denote $\frac{z}{2 x^6}=p$.

$$4t^5+10t^4+10t^3+5t^2+t= p \tag{1}$$

Wolfram Alpha really gives all five solutions in terms of hypergeometric functions. One doesn't explicitly contain the imaginary unit:

$$t_1 = -4 p~ {_4 F_3} \left(\frac15, \frac25, \frac35, \frac45;\frac12, \frac34, \frac54;50000 p^4\right) - \frac12$$

The other solutions contain the generalized hypergeometric function as well. If you want to know why this particular function solves quintic equation, I found a paper about it: https://arxiv.org/abs/math/0005026.

That the solution "looks real" doesn't mean $t_1$ it's necessarily real though. If the argument is greater than $1$, then this solution will be complex, which comes from the properties of hypergeometric functions.

Going back to $y$, we obtain:

$$y_1 = -4 x p~ {_4 F_3} \left(\frac15, \frac25, \frac35, \frac45;\frac12, \frac34, \frac54;50000 p^4\right) - \frac{x}2$$

We can treat $x,p$ as independent variables here, which gives us a nice explicit expression.

Let's denote $u=50000 p^4$, then we can check that the hypergeometric function takes the following range of values:

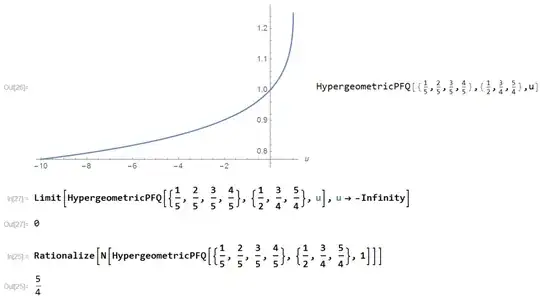
enter image description here

We can try finding some combinations of $x,z$ which give us positive integers for $y$, but I'm not sure how to do that in a systematic way.

Also, again, we should check all five solutions, because it's possible that the other four also give integers, if the imaginary part cancels out due to hypergeometric functions taking complex values.

Another idea is to look for rational roots of (1), using the rational root test (https://en.wikipedia.org/wiki/Rational_root_theorem).

It will only work if we take $p$ to be an integer, and then check if any of the factors of $p$ divided by $1,2,4$ (the factors of the leading term coefficient) work as solutions.

It's only useful for guessing though, since it doesn't guarantee that the number chosen that way will be a solution.

By the way, let's use Wolfram's advice to simplify the equation and introduce a new variable:

$$s=t+\frac12, \qquad t=s-\frac12$$

Substitution gives us:

$$\color{blue}{4 s^5- \frac{s}{4}=p} \tag{2}$$

$$s \left(s-\frac{1}{2} \right)\left(s+\frac{1}{2} \right)\left(s^2+\frac{1}{4} \right)=\frac{p}{4}$$

Now this is what I call a simplification! I'm sure it's not that hard to find rational roots for this equation.

To get back to the original variable, we use.

$$y=x \left(s-\frac{1}{2} \right)$$

Yuriy S
  • 31,474