I am reading on the Horseshoe map, but all I have found are qualitative explanations. These are great, but I think I would understand it better if I also had access to an example with an explicit function $f(x,y)$.
The way my professor explained it is the most explicit I have found:
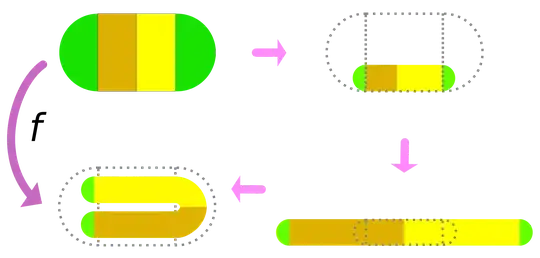
Consider some square $W$. The horseshoe map is continuous and injective on $\mathbb{R}^2$. In $W$, it contracts distances horizontally by $\delta < 1/2$ and expands vertically by $1/\delta$. Outside $W$, the only restriction is that $F$ is continuous and injective.
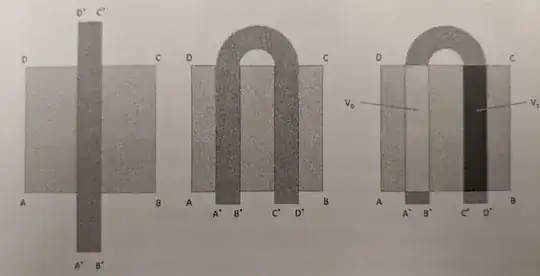
Now, I am trying to understand how this maps the following rectangle into a horseshoe:
Here, the square $W$ is defined by the corners $A,B,C,D$ and the function acts on the rectangle defined by $A^*,B^*,C^*,D^*$.
First, we need to stretch the region inside $W$. This will just stretch this region vertically, and the position of the left side (and the right side) gets shifted to the left according to $\delta$. Now, since the only constraint outside $W$ is being injective and continuous, do we attach the parts of the initial rectangle that were outside of $W$ onto the new rectangle? Moreover, how does this explain the bending? Does the arc have to have that shape or can it be any other shape as long as it stays injective and continuous (for example, instead of having that half-annulus can we have a rectangle that curves at a right angle to the right outside of $W$ and then it has another sharp $90$ degree curve to the right, heading into $W$. Basically, the rectangle would be transformed into the shape: $\sqcap$)?