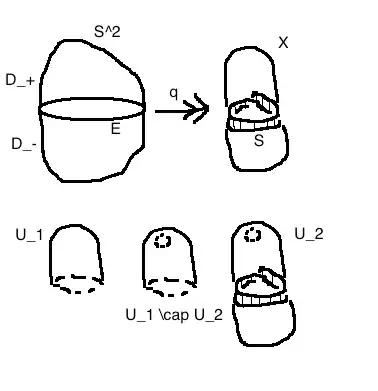
To make my notation clear I will state the problem like this:
Let $S^2 \subset \mathbb{R}^3$ be the unit sphere, and consider the equator $E = \{(x, y, z) \in S^2\ |\ z = 0\}\cong S^1$. Then we construct the quotient space $X = S^2 / \sim$, where $v \sim w$ iff $v,w\in E$ and $w = -v$. Compute $\pi_1(X)$.
Just like John Hughes suggests in his hint, the result is actually two copies of $\mathbb{R}P^2$ attached along essential loops, and we can use Seifert-van Kampen to compute $\pi_1$.
Describing $X$ in terms of $\mathbb{R}P^2$'s:
Let $q\colon S^2 \to X$ denote the quotient map, and let $S= q(E)$. Then $S = \mathbb{R}P^1 \cong S^1$.
If we restrict the quotient map $q\colon S^2 \to X$ to the upper hemisphere $D_+ = \{ (x, y, z) \in S^2\ | \ z \geq 0\}$, then topologically we're looking at a copy of $D^2$ whose boundary is glued to itself via the antipodal map, and therefore results in $\mathbb{R}P^2$. Let $q_+\colon H_+ \to X_+ \cong \mathbb{R}P^2$ denote the restricted quotient map, and notice $S= q_+(E)$. We can model this as a CW complex by attaching a $D^2$ to $S^1$ (representing $S$) by a map of degree $2$ on the boundary. If we restrict the quotient map to the lower hemisphere $q_-\colon D_- \to X_-$ then again we get a copy of $\mathbb{R}P^2$, and we have $X = X_+\cup X_-$ and $X_+ \cap X_- = q(E) \cong \mathbb{R}P^1$. In other words, $X$ is a union of two subspaces homeomorphic to $\mathbb{R}P^2$ whose intersection is the common subspace $\mathbb{R}P^1$. The CW model for $X$ then looks like a circle representing $S$ and then two disks attached to it via maps of degree $2$ on their boundaries.
Computing $\pi_1(X)$:
If $N \in X$ denotes the image of the north pole, then we can decompose $X$ into open sets $U_1 = q(int(D_+))\simeq\ast$ and $U_2 = X \setminus \{N\}\simeq q(D_-) \cong \mathbb{R}P^2$, where $U_1 \cap U_2 \simeq S^1$ (see Fig 1). Therefore the Seifert-van Kampen theorem describes $\pi_1(X)$ as the free product
$$ \pi_1(X) \cong \pi_1(\ast)\ast_{\pi_1(S^1)} \pi_1(\mathbb{R}P^2) \cong 1\ast_{\mathbb{Z}}\mathbb{Z}/2 , $$
where the homomorphism $\pi_1(S^1) \to \pi_1(\mathbb{R}P^2)$ is trivial because a generator of $\pi_1(U_1\cap U_2)$ wraps twice around $S$, and this loop is null-homotopic in $q(D_-)$ since $\pi_1(\mathbb{R}P^2)\cong \mathbb{Z}/2$. Therefore the free product is
$$ \pi_1(X) \cong \mathbb{Z}/2.$$
Fig 1.