Is this a decreasing sequence?

Question

In this nice question , the OP asks, or wants to prove that the sequence: $$a_{n+1} = \sqrt[n]{a_{1}+\dots+a_{n}}, \\a_1=1$$ is increasing. After playing a bit with Mathematica Cloud I realised that this is not the case as you may see in the following diagram: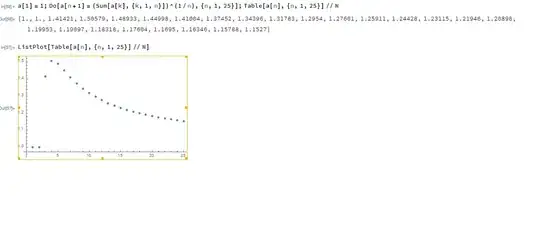 Actually, it seems that it is decreasing for $n> 4$. I have tried to prove it with induction and some other basic methods but I find it hard....Any hints, suggestions, please? Note that if it is decreasing there should be a limit and this limit should be $1$ as stated in these answers .

Answer 1

Note that $a_1+ \ldots + a_{n-1}=a_n^{n-1}$. So the recurrence relation is $a_{n+1}=\left(a_n^{n-1}+a_n\right)^{1/n}$.

So $a_{n+1}^n=a_n^{n-1}+a_n$.

So, now, denote as $x_{n+1}$ the root in $(1,\infty)$ of $x^n-x^{n-1}-x$, so that $y^n > y^{n-1}+y$ if $y > x_{n+1}$ and $y^n< y^{n-1}+y$ if $1 < y < x_{n+1}$.

Clearly, the sequence $x_n$ decreases. Now, assume $n \geq 3$: $a_{n+1} \geq x_{n+1}$ iff $a_{n+1}^n \geq a_{n+1}^{n-1}+a_{n+1}$ iff $a_n^{n-1}+a_n \geq a_{n+1}^{n-1}+a_{n+1}$ iff $a_n \geq a_{n+1}$.

Now, assume $a_{n+1} \geq x_{n+1}$: then $a_{n+1}^n-a_{n+1}^{n-1} \geq a_{n+1}$. So $a_{n+1}^{n+1}-a_{n+1}^n \geq a_{n+1}^2$ ie $a_{n+1}^{n+1}-a_{n+2}^{n+1}+a_{n+1} \geq a_{n+1}^2$. Therefore, $a_{n+2} < a_{n+1}$ and $a_{n+2} \geq x_{n+2}$.

So if $n \geq 4$ is such that $a_n \geq x_n$ (or $a{n-1} \leq a_n$) then for all $m \geq n$, $a_m \geq x_m$, hence $a_{m+1} \leq a_m$. The rest is simply a matter of computing the first terms to find the first point of non-increase.

Answer 2

For any integer $m \geqslant 3$, \begin{align*} \left(1 + \frac1m\right)^m & = 1 + \binom{m}1m^{-1} + \binom{m}2m^{-2} + \cdots + m^{-m+2} + m^{-m} \\ & \leqslant 1 + 1 + 1 + \cdots + \frac1m + \frac1m \quad (m + 1 \text{ terms}) \\ & < m. \end{align*} Therefore, $(m + 1)^m < m^{m+1}$. (I'm almost sure I once gave a shorter proof of this on MSE! $\ldots$ Apparently not. See the comments.)

That is, $n^{n-1} < (n - 1)^n,$ for every integer $n \geqslant 4.$

Equivalently, $$ n^{\frac{n-1}n} < n - 1 \quad (n \geqslant 4). $$

With $n$ any positive integer, let $f(x) = x^n - x^{n-1}.$ Then $$ f'(x) = nx^{n-2}\left(x - 1 + \frac1n\right) > 0 \text{ if } x \geqslant 1, $$ so $f(x)$ is strictly increasing for $x \geqslant 1.$

(That, too, must surely have a nicer proof. $\ldots$ Indeed it has. See the comments.)

Therefore, if $n \geqslant 4$ and $x \geqslant \sqrt[n]n,$ \begin{align*} x^n - x^{n-1} & \geqslant n - n^{\frac{n-1}n} \\ & > 1, \\ \therefore\ x^{n+1} - x^n & > x. \end{align*}

Take $x = a_{n+1} \geqslant \sqrt[n]n.$

Then $a_{n+2}^{n+1} = x^n + x < x^{n+1},$ therefore $$ a_{n+2} < x = a_{n+1}. $$

It remains to verify $a_5 < a_4.$

We have $43^2 = 1849 > 1800,$ therefore $43 > 30\sqrt2$, therefore $$ 2 + \sqrt2 < 45 - 29\sqrt2 = (3 - \sqrt2)^3, $$ therefore $2 + \sqrt2 + \sqrt[3]{2 + \sqrt2} < 5,$ i.e. $a_5^4 < 5 < \frac{81}{16},$ therefore $$ a_5 < \frac32. $$

On the other hand, we have $11^2 = 121 < 128,$ therefore $11 < 8\sqrt2,$ therefore $2 + \sqrt2 > \frac{27}8,$ therefore $$ a_4 > \frac32 > a_5. $$